Ecuación de restricción
El análisis cinemático en general se basa en el planteamiento y solución de ecuaciones cinemáticas VECTORIALES. De hecho en el análisis cinemático de mecanismos primero se debe resolver el problema de posición, posteriormente el de velocidad y por último el problema de aceleración.
Para resolver una ecuación cinemática, que es vectorial, se debe analizar componente por componente de la ecuación para determinar el número de incógnitas presentes, para ello recuerde que cada componente dispone de MAGNITUD y DIRECCIÓN, por lo que una ecuación cinemática tendrá solución si el número de incógnitas es solamente dos.
Aún cuando se disponga de una sola ecuación cinemática y dos incógnitas, se dice que tiene solución ya que una ecuación vectorial puede descomponerse en dos ecuaciones algebraicas al separar las componentes rectangulares X e Y.
Como el primer paso en el análisis cinemático es resolver el problema de posición, se pueden tener dos escenarios:
Para el caso del problema de posición se efectuará por técnicas analíticas, será necesario determinar ecuaciones vectoriales de posición que contenga elementos con el mayor número de datos conocidos. Una técnica para determinar esta ecuación se le conoce como ECUACION DE RESTRICCIÓN o también conocida como ECUACIÓN DE CIERRE.
Antes de explicar como deducir la ecuación de restricción primero se explicará como establecer el vector posición para diferentes casos en elementos de mecanismos.
Un mecanismo manivela-corredera como el de la Figura 1 será de utilidad para comprender la naturaleza de los vectores de posición.

Figura 1. Animación de un mecanismo RRRP
Vamos a establecer un vector posición que determine la posición del nodo A en función del nodo O2 y que se denotará como RA/O2, un vector posición que determine la posición de B en función de A RB/A , y otro que determine la posición del nodo B en función del nodo O2 RB/O2.
Por lo tanto, los vectores de posición se expresarán tal y como se muestra en la Figura 2
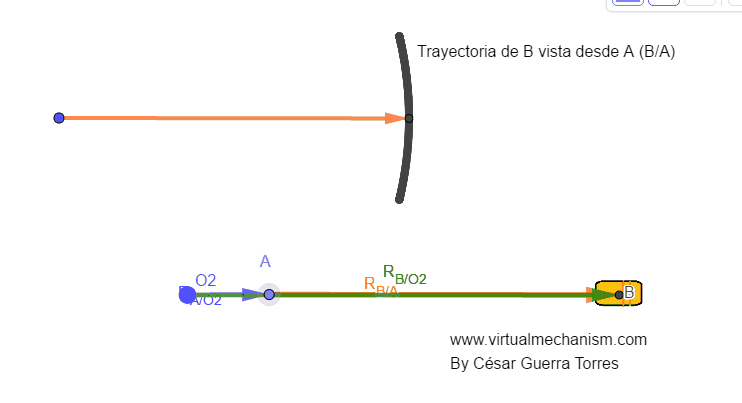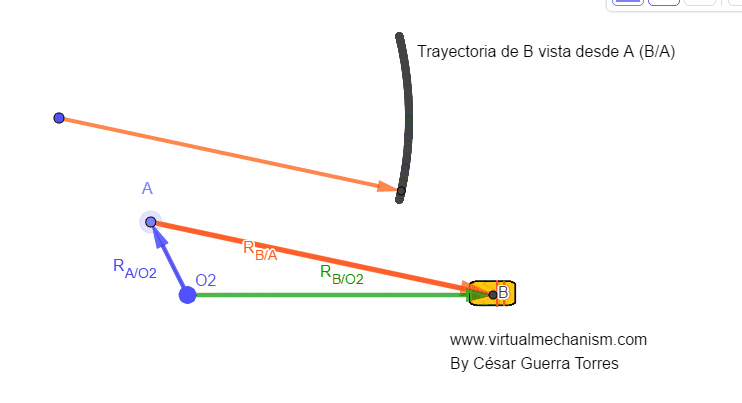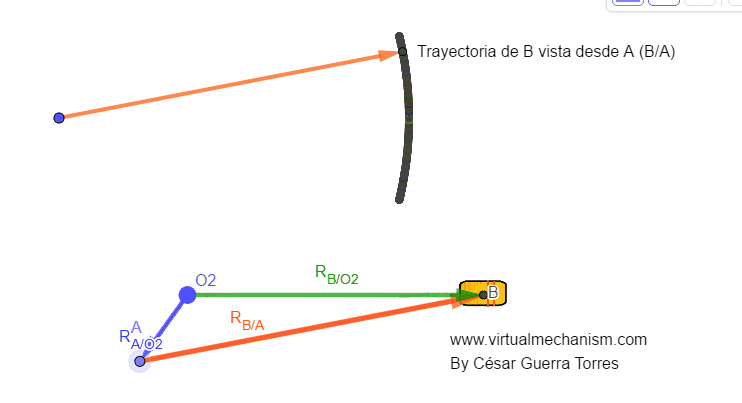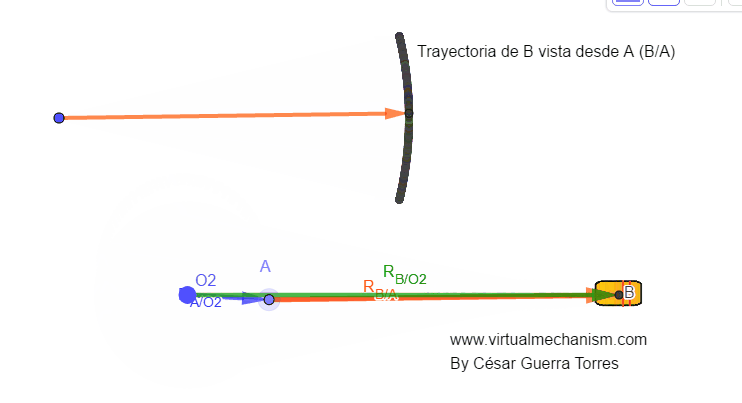
Figura 2. Vectores de posición.
Como se puede apreciar en la Figura 2, el vector RA/O2 , que puede reescribir solamente como RA ya que O2 es fijo, representa un vector posición para el movimiento de rotación absoluta (alrededor de un punto fijo); mientras que el vector RB/A representa un vector posición de movimiento también de rotación, solo que en este caso se le denotará como rotación relativa ya que como puede apreciarse en la animación de la Figura 2, es trayectoria circular.
Por último, el vector RB/O2 , que se puede reescribir solamente como RB representa un vector posición de movimiento traslación rectilínea.
Sólido rígido con par de revolutas.
Cuando se disponga de un sólido rígido, el vector posición de dos puntos del sólido rígido representará un vector posición de rotación. Ejemplo, en la Figura 2 se tiene que la manivela M2 y la biela B3 disponen de vectores posición con movimiento de rotación, donde la magnitud no cambia, pero la dirección si cambia.
Sólido rígido revoluta-prismático fijo.
Cuando se disponga de un sólido rígido con deslizamiento sobre un elemento fijo, el vector posición corresponderá al de un movimiento de traslación rectilínea, donde la magnitud del vector cambia, pero la dirección permanece constante.
Sólido rígido revoluta-prismático movil (Deslizamiento)
Este movimiento denota la combinación de los movimientos de rotación más traslación, por lo tanto el vector posición cambiara tanto en magnitud como en dirección. Un ejemplo de este tipo de movimiento es el conocido como mecanismo de deslizamiento puro, o bien (RRPR) como se muestra en la Figura 3.
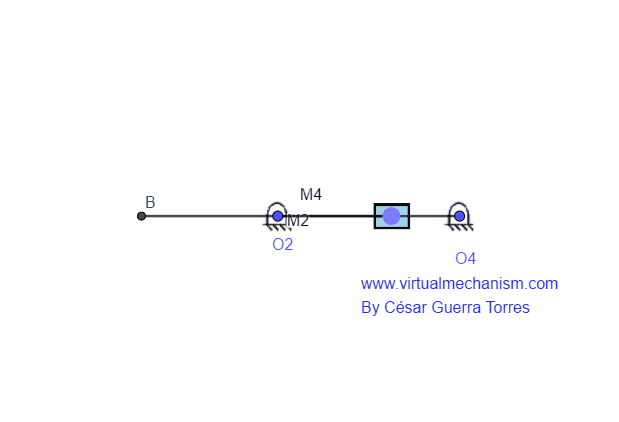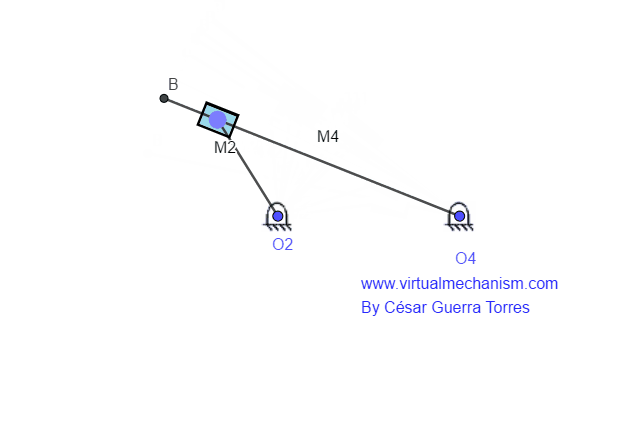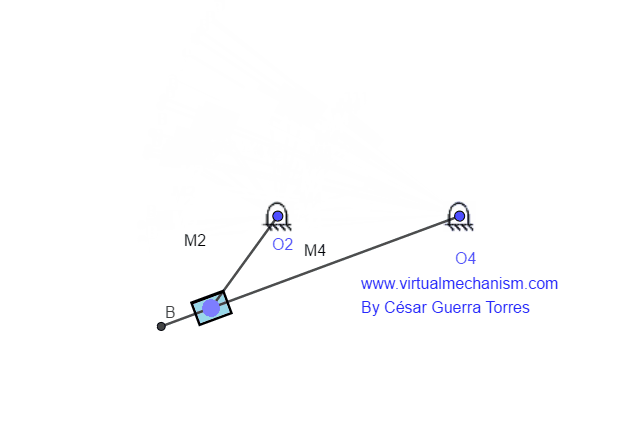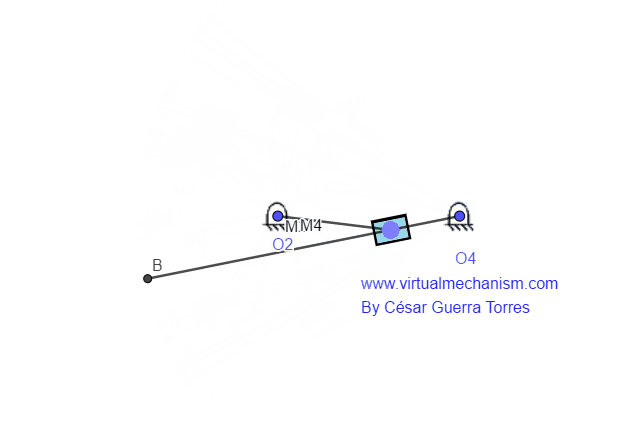
Figura 3. Mecanismo de deslizamiento (RRPR)
Por lo tanto, el vector posición del nodo A visto desde el pivote O2 denota al movimiento de rotación, propio de la manivela M2, PERO, el vector de posición del nodo A visto desde el pivote O4 denotará el movimiento de rotación y traslación, propio del collarín el cual se traslada sobre un elemento en rotación como se ilustra en la Figura 4.
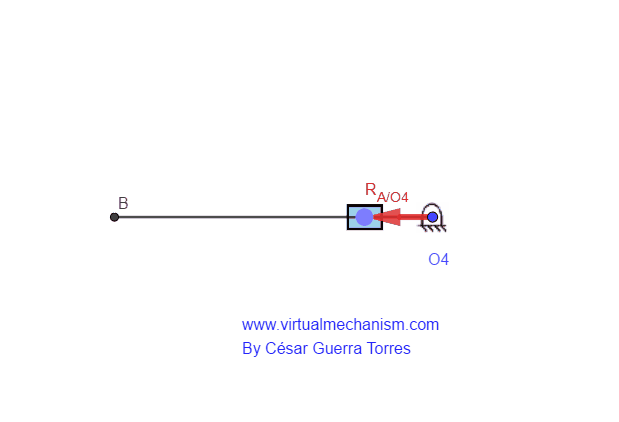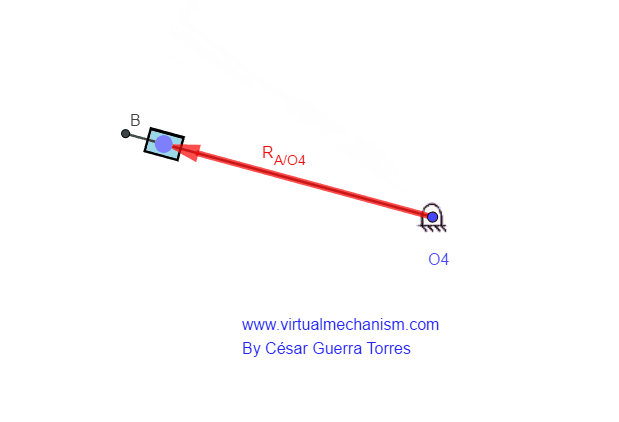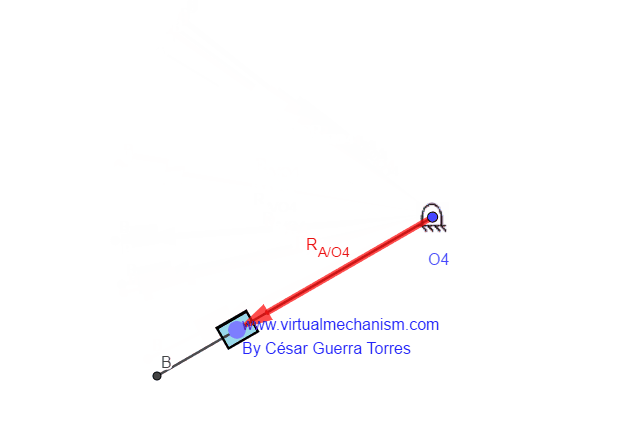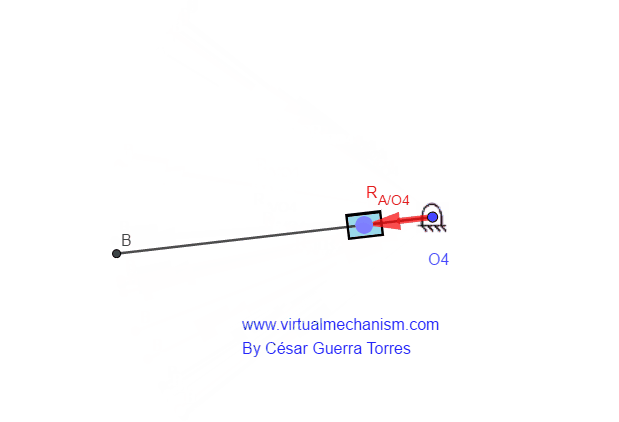
Figura 4. Vector posición con traslación y rotación.
Con lo anterior, es posible comprender la ecuación de restricción o de cierre para la solución del problema de posición, para ello considere el mecanismo de la Figura 5.
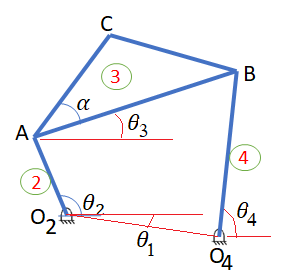
Figura 5. Mecanismo de cuatro barras.
Del mecanismo de la Figura 5 se dispone de todas las longitudes de los eslabones, así como las posiciones fijas O2 y O4, es decir, se conoce todos los datos de la topologia. Pero se desea establecer las posiciones de los eslabones; en este caso como el mecanismo es de un solo grado de libertad, entonces dada una coordenada, por ejemplo θ2, determinar el resto de las posiciones del mecanismo.
Como el dato es θ2 entonces se establece el vector posición RA/O2, posteriormente establecemos un vector de de posición para el AB, es decir RB/A, cuyo resultado es la posición del nodo B, es decir RB., el mismo procedimiento se utiliza para determinar la posición de C, tal como se muestra en la Figura 6.
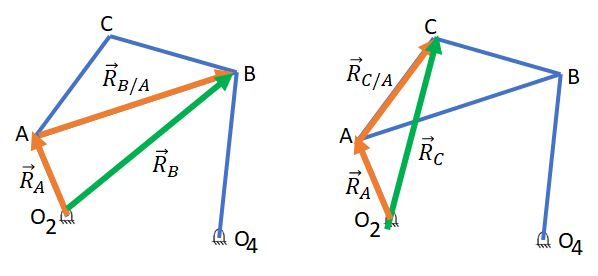
Figura 6. Vectores de posición.
Para cada caso de la Figura 6 se puede establecer una ecuaciones vectorial de posición de posición ya que en ambos casos se forma un cierre de vectores:
$$\vec{R}_B = \vec{R}_A + \vec{R}_{B/A}$$
$$\vec{R}_C = \vec{R}_A + \vec{R}_{C/A}$$
Con las observaciones anteriores, se reescriben las ecuaciones de posición colocando un punto o dos, indicando cuanto se desconoce de dicho vector:
$$\ddot{\vec{R}}_B = \vec{R}_A + \dot{\vec{R}}_{B/A}$$
$$\ddot{\vec{R}}_C = \vec{R}_A + \dot{\vec{R}}_{C/A}$$
Sin embargo en ambas ecuaciones se tienen tres incógnitas, lo que imposibilita la solución, como por ejemplo, por descomposición rectangular que requieres solo dos incógnitas.
Una solución ahora es establecer el camino vectorial alterno como se muestra en la Figura 7
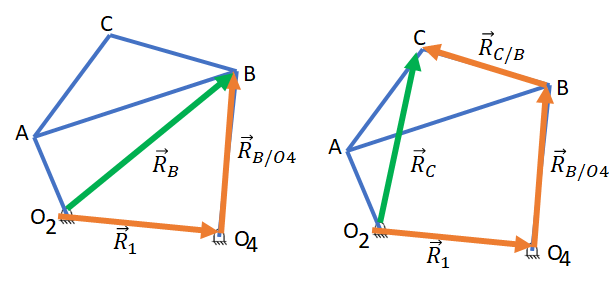
Figura 7. Vectores de posición alternos.
Con las observaciones anteriores se puede establecer otras ecuaciones de posición para determinar $\vec{R_B}$ y $\vec{R_C}$
$$\ddot{\vec{R}}_B = \vec{R}_1 + \dot{\vec{R}}_{B/O_4}$$
$$\ddot{\vec{R}}_C = \vec{R}_1 + \dot{\vec{R}}_{B/O_4} + \dot{\vec{R}}_{C/B}$$
Igualando las ecuaciones de posición para ambos casos se tiene:
$$ \vec{R}_A + \dot{\vec{R}}_{B/A} = \vec{R}_1 + \dot{\vec{R}}_{B/O_4}$$
$$ \vec{R}_A + \dot{\vec{R}}_{C/A} = \vec{R}_1 + \dot{\vec{R}}_{B/O_4} + \dot{\vec{R}}_{C/B}$$
Como puede apreciarse en las ecuaciones anteriores, la primer ecuación tiene dos incógnitas, por lo que tiene solución; mientras que la segunda ecuación tiene tres incógnitas e inicialmente no tiene solución.
En efecto, una vez que se solucione la primer ecuación se dispondrán de datos para determinar el vector $\vec{R}_C$ como es el ángulo θ3.
Con lo anterior, se puede establecer de una manera más simple cual sería el orden para establecer una solución en un mecanismo de n.-barras. En la Figura 5 se puede apreciar que el mecanismo inicial lo forman los eslabones del cuadrilátero O2,A,B,O4; es decir, si se quitan los eslabones CA y CB el mecanismo no pierde su condición de movilidad, por lo tanto es notorio que el nodo C depende del nodo A y B, y no puede determinarse su posición sin antes resolver el nodo B.
Created with the Personal Edition of HelpNDoc: Free Kindle producer