Posición

Análisis de posición

El análisis de posición en mecanismos se puede deducir de la siguiente forma: "Disponiendo de la topología de un mecanismo, entonces dada la(s) posición(es) de un(os) del (los) elemento(s) del mecanismos,  determinar la posición del resto de los eslabones, por lo general, solo se desea determinar la posición del eslabón conocido como eslabón de salida".

El porque pueden ser diversas posiciones como entrada, se debe a el grado de libertad del mecanismo, por lo que un mecanismo de un grado de libertad requiere impulsar un solo elemento para mover el resto de los eslabones, de dos grados de libertad requiere de dos y así sucesivamente.

El análisis de posición se puede ejemplificar como se muestra en la Figura 1, donde la variable de salida es la posición de uno de los eslabones denotada por la variable sf, mientras que la variable de entrada es la posición de otro de los eslabones denotada por la variable si. 

Aquí el objetivo es determinar la ecuación que relacione la posición de salida vs. entrada sf=f(si).

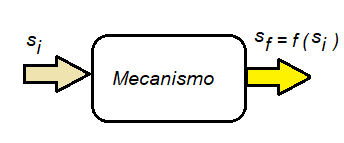
Figura 1. Representación del problema de posición.

Es importante aclarar que en algunos mecanismos, como los mecanismos de barras articuladas, se tiene que para una coordenada de entrada se pueden tener dos soluciones de posición, esto se demostrará en forma sencilla usando el método gráfico para el análisis de posición, sin embargo, se puede adelantar que en este tipo de mecanismos, la ecuación de posición se puede reducir a una forma cuadrática, lo que evidentemente genera dos soluciones posibles para una misma entrada.

Para comprender el problema de posición considere la Figura 2 que muestra la animación de un mecanismo manivela-corredera mostrando como dato de entrada la coordenada de posición de la manivela θ2, mientras que la coordenada de salida es representada por la coordenada de posición de la corredera RB.

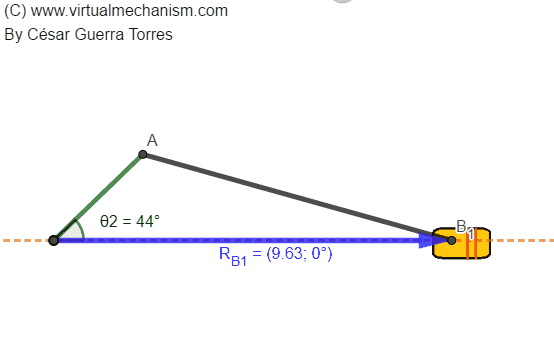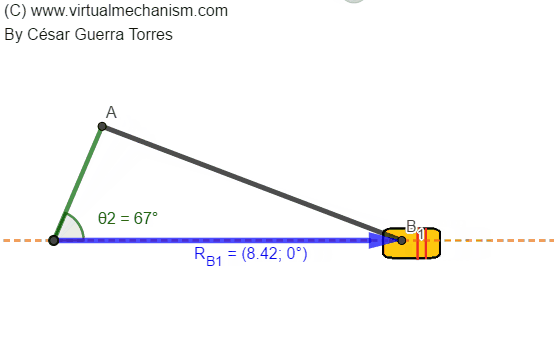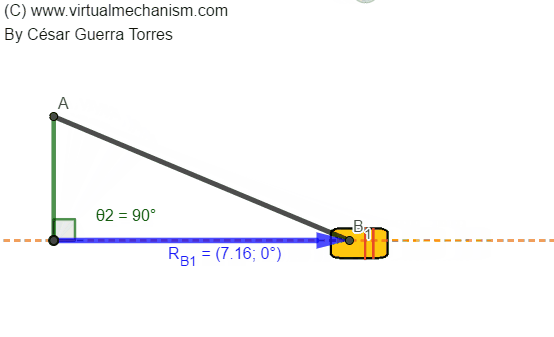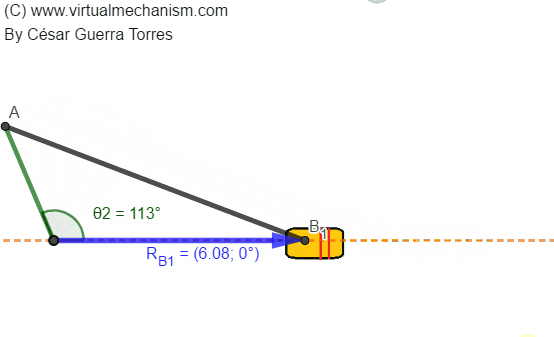
Figura 2. Coordenadas de entrada y salida en un mecanismo manivela-corredera

Created with the Personal Edition of HelpNDoc: Easily create iPhone documentation