Conceptos matemáticos
El análisis cinemático de mecanismos se puede realizar desde dos perspectivas matemáticas, el análisis vectorial y el análisis geométrico. Ambos nos permiten dar solución a problemas de análisis, pero se puede mencionar que el uso de herramientas geométricas se enfocan más bien para estrategias de diseño así como de implementación computacional.
DEDUCCIÓN MEDIANTE EL ALGEBRA VECTORIAL
Considere la representación gráfica de un vector de posición como se muestra en la Figura 1.
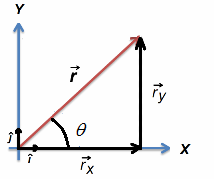
Figura 1. Representación gráfica de un vector.
$$\overrightarrow{r}=\overrightarrow{r}_x +\overrightarrow{r}_y$$
$$\overrightarrow{r}=rcos(\theta )\widehat{i} + rsen(\theta )\widehat{j}$$
$$\overrightarrow{r}=r(cos(\theta )\widehat{i} + sen(\theta )\widehat{j})$$
Si se define $\overrightarrow{\lambda} _\theta =(cos(\theta )\widehat{i} + sen(\theta )\widehat{j})$ como el vector direccionador unitario, entonces se tiene la siguiente expresión vectorial:
$$\overrightarrow{r}=r\overrightarrow{\lambda }_\theta$$
Esta última ecuación puede ser usada para denotar en forma vectorial la posición de una partícula, dicha expresión se compone de la magnitud r, y la dirección $\overrightarrow{\lambda }_\theta$.
$$\overrightarrow{\lambda}_\theta =cos\theta \widehat{i}+sen\theta \widehat{j}$$ $${\overrightarrow{\lambda}_\theta}'=\partial\overrightarrow{\lambda}_\theta/\partial \theta =-sen\theta \widehat{i}+cos\theta \widehat{j}$$ $${\overrightarrow{\lambda}_\theta}''=\partial^2\overrightarrow{\lambda}_\theta/\partial\theta^2 =-cos\theta \widehat{i}-sen\theta \widehat{j}$$ |
Ec 1 |
Para poder establecer las ecuaciones de velocidad y aceleración es importante primero establecer la derivada del vector direccionador $\overrightarrow{\lambda }_\theta$ con respecto a la variable θ.
Haciendo uso de algunas propiedades trigonométricas, las ecuaciones escritas con anterioridad se pueden reescribir de la siguiente manera:
$$\overrightarrow{\lambda}_\theta =cos\theta \widehat{i}+sen\theta \widehat{j}$$ $${\overrightarrow{\lambda}_\theta}'=cos(\theta+90^o) \widehat{i}+sen(\theta+90^o)\widehat{j}$$ $${\overrightarrow{\lambda}_\theta}''=cos(\theta+180^o) \widehat{i}+sen(\theta+180^o)\widehat{j}$$ |
Ec 2 |
Lo anterior tiene un importante significado.
NOTA 1.
Al derivar el vector direccionador con respecto a la variable $\overrightarrow{\lambda }_\theta$ se tiene como resultado girar dicho vector noventa grados en el sentido de como se esta midiendo el ángulo θ.
Esto es de importancia en el análisis cinemático, ya que para obtener la velocidad o aceleración de una particula se debe derivar el vector de posición primero conrespecto a la variable θ, posteriormente derivar θ con respecto al tiempo. Lo anterior nos tendrá que definir la magnitud de los vectores de velocidad y aceleración, así como sus direcciones, tal y como se muestra a continuación.
Created with the Personal Edition of HelpNDoc: Easily create CHM Help documents