En algunos diseños geométricos de mecanismos, se tiene la necesidad de mover un mecanismo en dos posiciones extremas, en donde para su operatividad se requiere un elemento motriz que permita mover un oscilador en dos posiciones extremas. Aunque es posible solucionar este problema con un motor controlado por sensores, o bien el uso de servomotores, esto puede resultar impráctico o costoso; a cambio de esta solución se puede utilizar otro par de eslabones, llamados diadas, para poder controlar la oscilación mientras que la entrada se conecta a un motor el cual podrá dar revoluciones completas.
Una manera de solucionar la necesidad de síntesis de oscilación, con posiciones extremas, es mediante el diseño de diadas, las diadas no son mas que un par de eslabonamientos que se integrará a un mecanismo, por ejemplo, se puede tener una diada impulsara formada por una manivela y una biela como se muestra en la figura 1.B
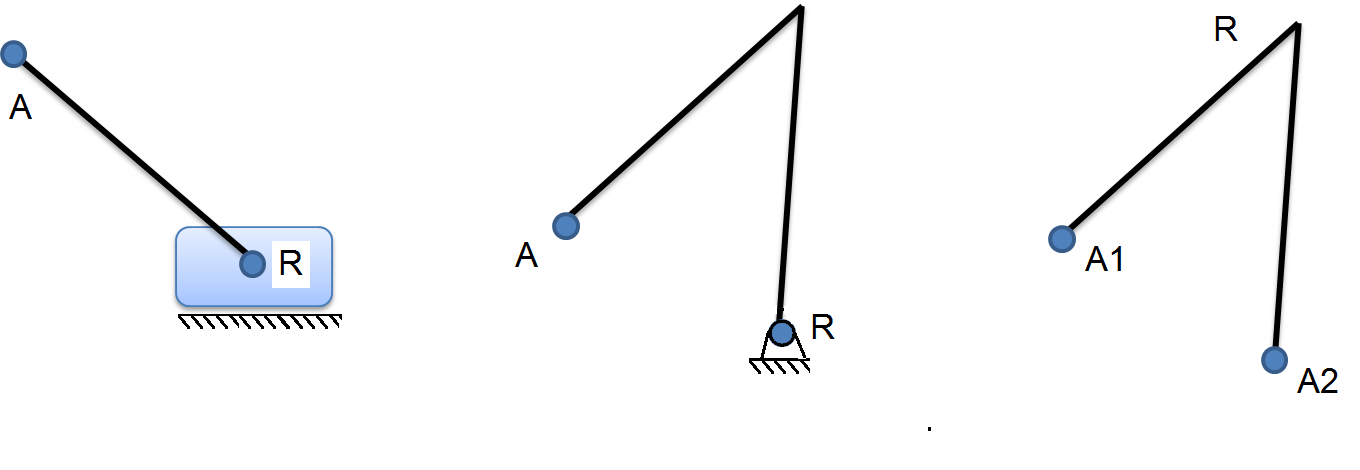
Figura 1. Tipos de diada (A) Biela-corredera, (B) Biela manivela, (C)Biela-biela.
Antes de exponer el procedimiento para el diseño de diadas, es importante mencionar un parámetro que influye en la estrategia de implementación para diseñar osciladores con posiciones extremas o "topes". Este parámetro se le conoce como relación de transmisión.
La relación de transmisión (Q) es un parámetro que relaciona el tiempo de avance y retroceso en un oscilador, de modo que si Q=1, indica que el tiempo de avance es igual al tiempo de retroceso en un oscilador. Por lo tanto, la relación de transmisión Q está definida como:
$$Q=\frac{tav}{tret}$$
Donde tav es el tiempo de avance y tret es el tiempo de retroceso como se muestra en la Figura 2
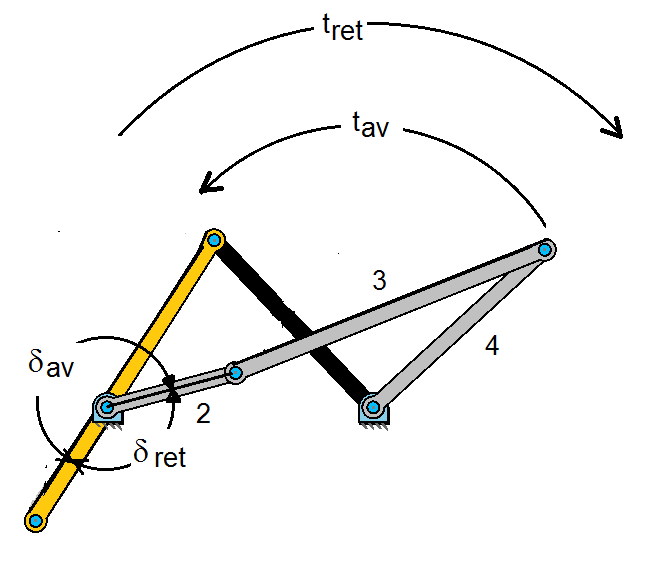
Figura 2. Avance y retroceso
El mismo parámetro se puede obtener usando los ángulos diferenciales de la siguiente forma
$$Q=\frac{\delta _{av}}{\delta _{ret}}$$
Por lo tanto si Q>1 indica que el tiempo de retroceso es menor que el tiempo de avance, a este tipo de mecanismos se les conoce como mecanismo de retorno rápido.
Necesidad: Se desea desplazar un oscilador con pivote O4 en sus dos posiciones extremas $\theta _{INI}$ y $\theta _{FIN}$. Determine las longitudes de la diada impulsara manivela-biela que permita desplazar el objeto en ambas posiciones .
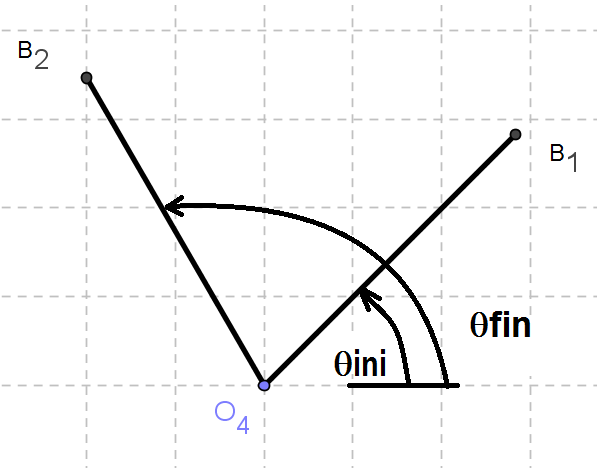
Figura 3. Condiciones extremas de oscilación de diseño
Requerimiento de la síntesis: El ángulo de oscilación ó el angulo inicial y final de la oscilación, la longitud del oscilador y las coordenadas o posición del pivote del oscilador.
Resultado: El resultado de la presente síntesis se deberá tener los siguientes parámetros, mismos que se muestran en la Figura 4.
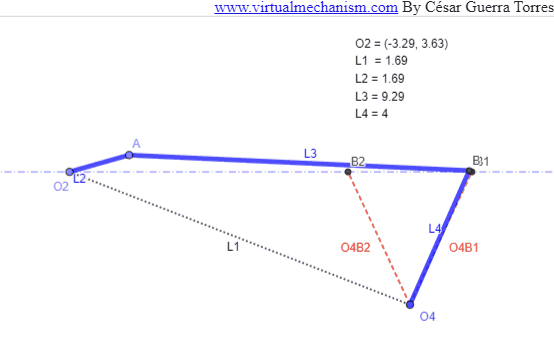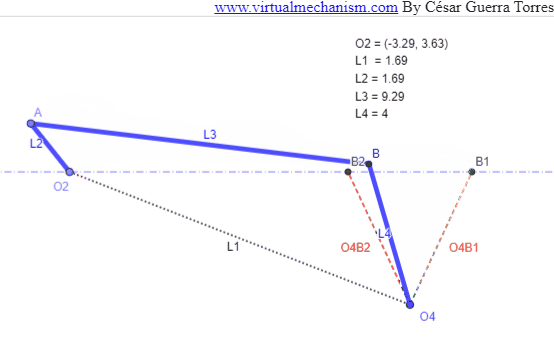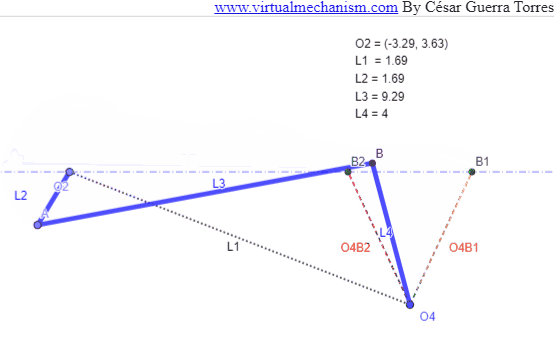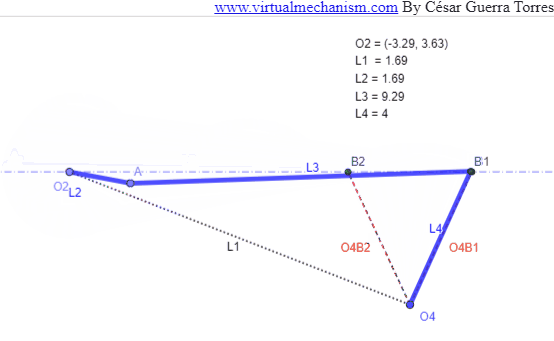
Figura 4. Oscilador con Q=1.
Parámetro |
Valor |
Coordenadas del rotopolo O2 |
|
Coordenada del rotopolo O4 |
|
Longitud manivela O2A |
|
Longitud biela AB |
|
Longitud del oscilador O4B |
Tabla 1. Tabla de resultados.
El diseño de diadas para impulsar osciladores puede realizarse cuando en conjunto forman un mecanismo manivela oscilador con Q=1 o Q diferente a la unidad, primero se explicará el procedimiento para sintetizar una diada impulsora con Q=1, es decir, el tiempo de oscilación es el mismo tanto avance como retroceso.
Considere un oscilador cuya necesidad de oscilación en los extremos es de θini y θfin como se muestra en la Figura 3. Para iniciar el procedimiento de síntesis seleccione la ubicación de O4 en un punto arbitrario, o bien en un unas coordenadas si es que se proporcionó; trace los extremos O4B1 y O4B2 usando la longitud del oscilador.
Ahora trace una línea de construcción que pase por B1 y B2. sobre la misma seleccione un punto arbitrario O2 y que será el pivote de la manivela impulsora como se muestra en la Figura 4
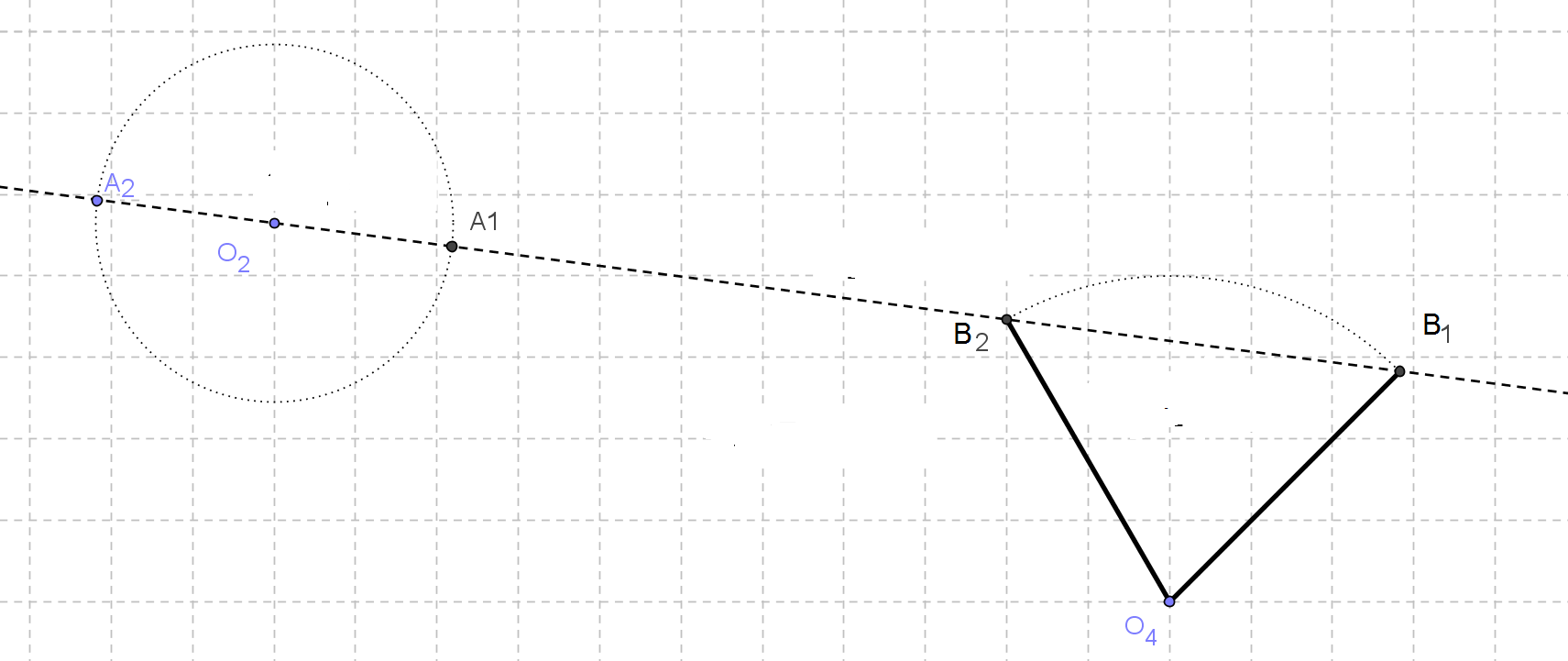
Figura 5 Construcción de la diada con Q=1
Una vez lo anterior, las longitudes de los eslabones quedarán definidas midiendo los siguientes segmentos:
Una vez obtenido las longitudes de los eslabones es necesario verificar que el cuadrilátero cumpla con la la condición de Grashof
L1+L2 < L3 + L4
Si no cumple con la condición de Grashof, hay que cambiar la selección de O2, y volver a verificar la misma
2.2 Método analítico.
2.3 MWS
Created with the Personal Edition of HelpNDoc: Free PDF documentation generator