Conceptos metemáticos de la síntesis posicional
Una de las estrategias matemáticas en la síntesis cinemática consiste en localizar el centro de una o varias circunferencias afines a dos o tres puntos en su perímetro. De modo que para dos puntos en un plano cartesiano el centro de una circunferencia que pase por esos dos puntos, que llamaremos P1 y P2, estará localizado sobre la mediatriz de dichos puntos como se muestra en la Figura 1.
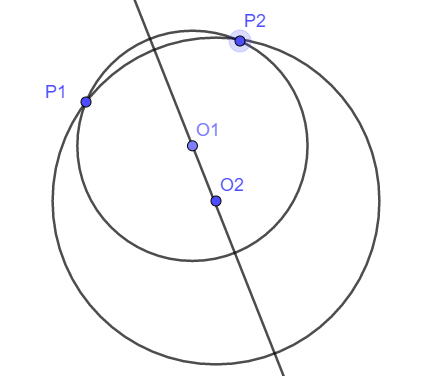
Figura 1. Centro de circunferencia (rotopolo) para dos puntos.
De la Figura 1 se puede dibujaron solo dos circunferencias con centro O1 y O2, ambas circunferencias tienen en común los puntos P1 y P2 en su perímetro, es decir, existe un número infinito de circunferencias que pasan por los puntos P1 y P2, todas con centro localizado en la mediatriz.
De la Figura 1 se concluye que por dos puntos pasan un número infinito de circunferencias cuyo centro estará localizado sonre la mediatriz de dichos puntos. Pero si en lugar de dos puntos, se desea determinar cuantas circunferencias pasan por tres puntos A,B y C la respuesta es UNA, y el centro estará localizado en la intersección de la mediatriz AB y BC como se muestra en la Figura 2.
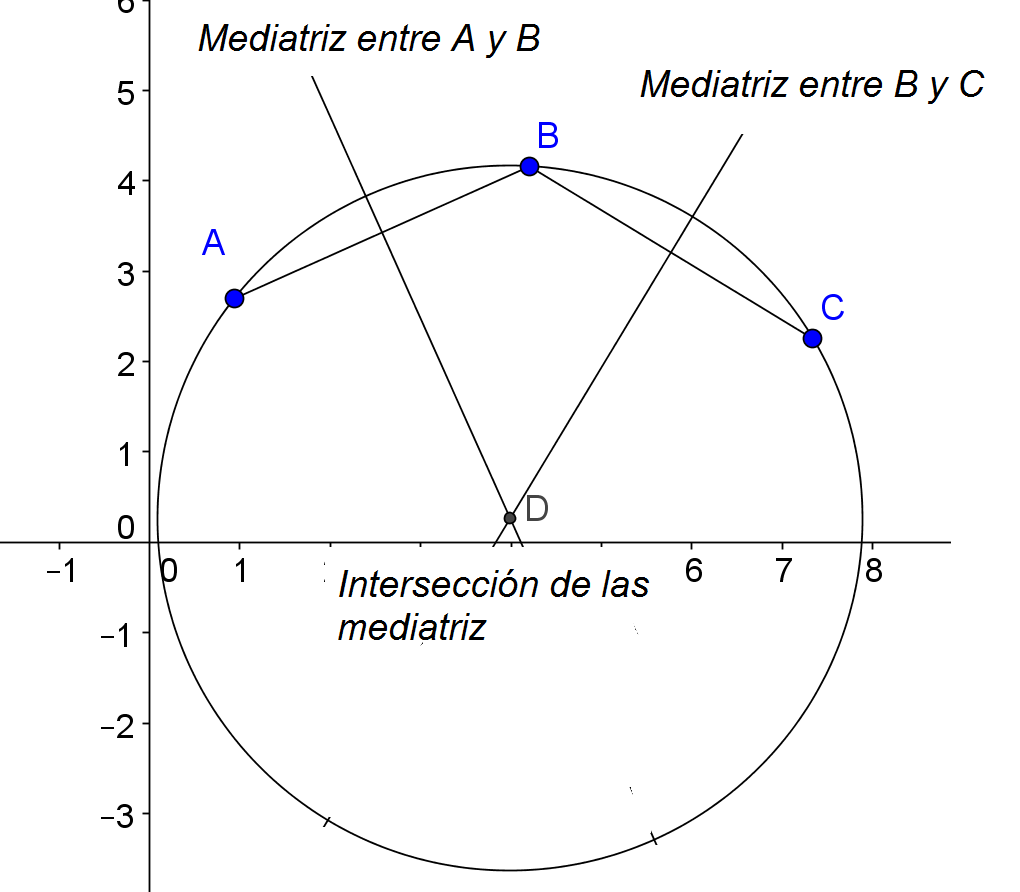
Figura 2. Centro de circunferencia (rotopolo) para tres puntos.
Para las demostraciones analíticas o desarrollo de la síntesis usando ecuaciones geométricas se hará uso de las siguientes definiciones y nomenclatura.
Distancia entre dos punto $\bar{BA} $.
Sea A y B dos puntos en un plano cartesiano con coordenadas A(ax,ay) y B(bx,by), por lo tanto, la distancia $\bar{BA} $ entre estos dos puntos es una cantidad escalar definida por.
$$\bar{BA} = \sqrt{(bx-ax)^2+(by-ay)^2 }$$
Pendiente entre dos puntos ($m_{BA} $).
Sea A y B dos puntos en un plano cartesiano con coordenadas A(ax,ay) y B(bx,by), por lo tanto, la pendiente $m_{BA} $ entre estos puntos es una cantidad escalar, la cual define el valor de la inclinación y queda determinada como:
$$m_{BA} =\frac{by-ay}{bx-ax}$$
Punto medio entre dos puntos ($M_{BA} $).
Sea A y B dos puntos en un plano cartesiano con coordenadas A(ax,ay) y B(bx,by), por lo tanto, la mediatriz entre estos puntos denota un punto M(mx,my) justo a la mitad del segmento formado por éstos puntos, cuyas coordenadas quedarán definidas como:
$$(mx,my) =(\frac{ax+bx}{2},\frac{ay+by}{2})$$
Ecuación de la recta ($l(x,y)$).
Sea una recta cuyos datos conocidos son la pendiente $m$ y una coordenada de un punto que pase por la mismos $O(x_0,y_0)$; por lo tanto la ecuación que define las coordenadas de cualesquier punto que pase por la misma P(x,y) esta definida como:
$$l(x,y) = (y-y_0) - m(x-x_0) = 0$$
Ecuación de la mediatriz ($l_\{perp}(x,y)$) de dos puntos.
Sean dos puntoa A(ax,ay) y B(bx,by) , la mediatriz entre estos dos puntos es una recta perpendicular que pasa por el punto medio de A y B; por lo tanto la recta de dicha mediatriz queda definida en función de las coordenadas del punto medio M(mx,my) mediante la siguiente ecuación:
$$ l_{\perp}(x,y) = (y-my) +\frac{bx-ax}{by-ay}(x-mx) $$
Coordenada de un punto B relativa a un punto A
Sea A(ax,ay) una coordenada conocida, y BA(bax,bay) la coordenada de un punto B relativa al punto A en forma rectangular, por lo tanto la coordenada absoluta del punto B(bx,by) se obtiene como:
$$B = A + BA$$
$$(bx,by) = (ax + bax,ay+bay)$$
Sea A(ax,ay) una coordenada conocida, y BA(L_{BA};\theta-{BA}) la coordenada de un punto B relativa al punto A en forma polar donde $L_{BA} denota el valor del segmento $BA$ y $\theta_{BA} el ángulo entre estos dos puntos; por lo tanto la coordenada absoluta del punto B(bx,by) se obtiene como:
$$B = A + BA$$
$$(bx,by) = (ax + L_{BA}cos(\theta_{BA}),ay+ L_{BA}sen(\theta_{BA}))$$
Created with the Personal Edition of HelpNDoc: Free iPhone documentation generator