ANTERIOR

html

Script 2. C.I. Como centro de rotación móvil

Tal como puede apreciarse en el script la ubicación de un C.I. puede variar dependiendo la posición del mecanismo, de allí su nombre de INSTANTÁNEO, ya que el análisis efectuado aplica a ese instante.

Centro Instantáneo por observación.

Resulta ser que un C.I. no tan solo son los pivotes o centros de giro, en realidad toda articulación en un mecanismo es un C.I. que asocia los dos eslabones de contacto y se denotará como OXY conde X e Y son los eslabones que asocia dicha articulación, en la Figura 1 se puede apreciar los centros instantáneos por definición en un mecanismo de 6 barras.

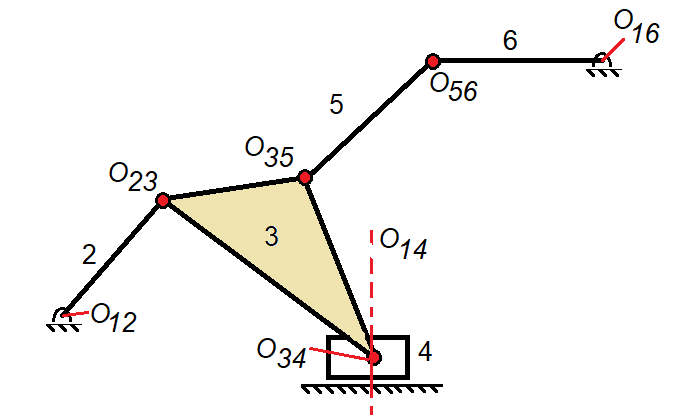
Figura 1. Centros instantáneo por observación.

Como puede apreciarse en la Figura 1, todas las articulaciones representan un C.I. que denota que eslabones estan conectados, O12 es un C.I. que denota la articulación entre el eslabón 2 y el fijo. Incluso se coloca el C.I. O14, el cuál tiende al infinito sobre la perpendicular al deslizamiento.

Centro instantáneo usando Círculo de Centros de Kennedy

En la Figura 1 es posible por observación determinar C.I. en un mecanismo, ya que cada articulación representa un C.I. Pero ahora suponga la necesidad de determinar los centros instantáneos O13 y O15, aunque físicamente no existe una articulación de la biela 3 y 5 con el elemento fijo, bajo esta estrategia gráfica es posible suponer tal afirmación.

Aunque es posible determinar los centros O13 y O15 tal como se explicó en el apartado anterior, es posible utilizar una estrategia gráfica conocida como Círculo de Centros de Kennedy , o simplemente Círculo de Centros para determinar no solo los centros de pivoteo O13 y O15, si no nodos de enlace que físicamente no existen, por ejemplo imagine en la Figura 1 determinar el instante O26, el cual establece un contacto instantáneo entre el eslabón 2 y 6, aunque éstos físicamente no estén conectados, !interesante! ,¿no?.

Para comprender la estrategia es importante citar un teorema llamado Teorema de Kennedy de los tres centros.

Teorema de Kennedy: Siempre que se tengan tres elementos en movimiento coplanario, existirá sobre una línea, llamada Línea de Kennedy, la ubicación de los tres centros instantáneos que relaciona los tres elementos.

Para comprender el teorema de Kennedy considere dos discos conectados entre sí y articulados al elemento fijo como se muestra en la Figura 2.

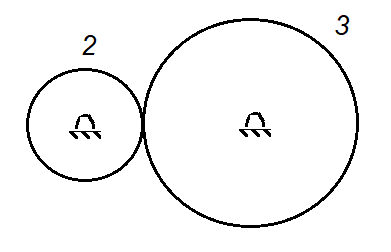
Figura 2. Tres eslabones con movimiento relativo 1,2 y 3.

Como toda articulación representa un C.I. entonces los C.I. de la Figura 2 relacionara los tres eslabones 1,23, es decir O12, O13 y O23 se encuentran sobre una línea como se muestra en la Figura 3

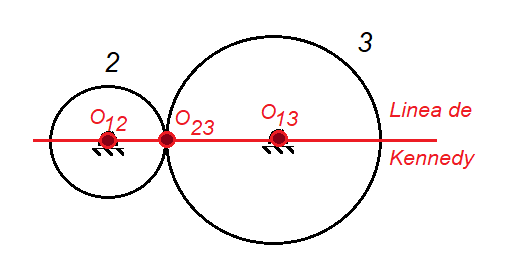
Figura 3, Línea de Kennedy.

La figura 2 y 3 sirven para explicar el teorema de Kennedy y la línea de Kennedy, se usaron discos para ejemplificar dicho teorema pero no corresponde con el concepto de Cïrculo de Kennedy.

El círculo de Centros es una herramienta gráfica visual que sirve para determinar C.I. que no se pueden obtener por observación cuyo procedimiento se describe a continuación:

1. Dibujar un circulo, a mano alzada recomendablemente en el mecanismo a analizar, éste círculo será llamado Círculo de Centros.
2. Distribuir uniformemente puntos sobre el Círculo de Centros, según el número de eslabones del mecanismo incluyendo el elemento fijo, en cada punto enumerar del 1 a n, donde n es el número de eslabones..
3. Determinar todos los C.I. por observación.
4. Unir en el Círculo de Centros dos puntos por medio de un segmento que indique el C.I. de dichos puntos es conocido.
5. Para determinar el C.I. desconocido trazar un segmento punteado que una los puntos que indiquen el C.I. a determinar
6. El C.I. desconocido se podrá localizar en el mecanismo si pertenece a un par de C.I. conocidos
7. Si el C.I. se puede localizar bajo el punto anterior, entonces localizarlo en el mecanismo trazando las rectas correspondientes, de modo que la intersección de dichas rectas, será el C.I. desconocido.

Por ejemplo, en el mecanismo de la Figura 1 se tienen los centros por definición y se desea determinar el C.I. O13. la Figura 4 describe el Círculo de Centros con los centros conocidos uniendo nodo con nodo, y se muestra el O13 uniendo 1 con 3 como desconocido.

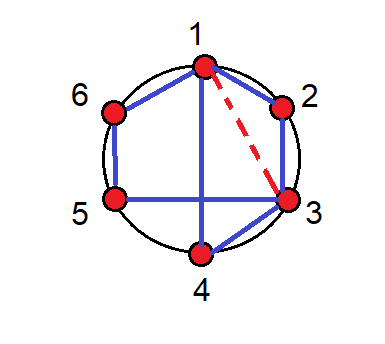
Figura 4. Círculo de Centros del Ejemplo 1.

De la Figura 4 se puede concluir que el centro O13 pertenece a O12 y O23, que son conocidos, asó como a O14,O34 que también son conocidos; ciertamente pertenece tambien a O16,O36, pero O36 no es conocido.

Por lo tanto, el centro O13 pasará por la línea de kennedy O12 y O23, así como la línea de Kennedy O14 y O34. En la Figura 5 se muestra la localización del centro O13 del mecanismo.

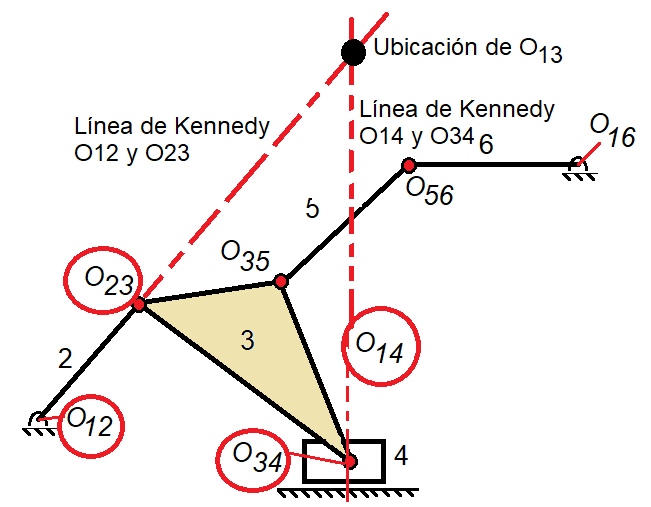
Figura 5. Localización de C.I usando líneas de Kennedy

Teorema de velocidades angulares

Ya visto la forma de determinar los C.I en un mecanismo, ahora procede explicar su utilización para determinar velocidades angulares desconocidas a partir de velocidades angulares conocidas.

Considere el mecanismo de discos de la Figura 3; sea $V_{O23}$ la velocidad de contacto, también conocida como Velocidad del centro común; dicha velocidad puede determinarse de dos maneras:

$$V_{O23} = (\omega_2)(r_{O12->O23})$$
$$V_{O23} = (\omega_3)(r_{O13->O23})$$

En base a lo anterior se puede formular el siguiente teorema:

Teorema de velocidades angulares. Sean X e Y dos eslabones con movimiento relativo coplanario con respecto al elemento fijo 1, sea $\omega_X$  y $\omega_Y$ las velocidades angulares de los eslabones, respectivamente, teniendo localizado la línea de Kennedy donde se ubican los centros instantáneos O1X, O1Y, OXY (no importa el orden) entonces:

$$\frac{\omega_X}{\omega_Y} = \pm \frac{r_{O1Y->OXY}}{r_{O1X->OXY}}$$

Donde $ r_{O1Y->OXY}$ denota la magnitud del radio desde el centro O1Y hasta el centro OXY, similarmente $ r_{O1X->OXY}$.

El signo $\pm$ se convierte en negativo si el centro común, OXY , se encuentra en medio de los dos centros de pivoteo O1X y O1Y ya que girarían opuestos, en caso contrario es positivo.

Una vez que se determina la velocidad angular desconocida, se puede determinar cualquier velocidad tangencial perteneciente a el eslabón. Por ejemplo, para el eslabón Y, la velocidad de cualquier punto Q se determinará

$$V_Q=(\omega_Y)(r_{O1Y->Q})$$

Procedimiento

1. Determinar los centros por definición
2. Establecer el eslabón de velocidad conocida $\omega_X$ y el eslabón de velocidad desconocida $\omega_Y$.
3. Usar la técnica de Círculo de Centros para determinar la línea de Kennedy en el mecanismo O1X, O1Y, OXY.
4. Usar el teorema de velocidades angulares para determinar la velocidad angular desconocida $\omega_Y$
5. Determine las velocidades tangenciales necesarias del eslabón $Y$ usando la ecuación $V_Q=(\omega_Y)(r_{O1Y->Q})$, donde $Q$ es cualquier nodo del eslabón $Y$.

Created with the Personal Edition of HelpNDoc: Easily create EBooks