Análisis de velocidad
El análisis de velocidad en mecanismos planos recide en determinar las velocidades angulares de las manivelas, las velocidades angulares de las bielas, así como las velocidades lineales (tangenciales) de los nodos de enlace entre eslabones.
Como los eslabones de un mecanismo cambian de posición en el tiempo, además la posición de los elementos de un mecanismo se representan con ecuaciones vectoriales, entonces es fácil deducir que la velocidad de los elementos de un mecanismo dependen además de los datos cinemáticos de velocidad, de la posición de los elementos del mecanismo, por lo que se concluye que antes de elaborar un análisis de velocidad, es necesario resolver el problema de posición en el mecanismo
Así como el análisis de posición es primordial para el análisis de velocidad, el análisis de velocidad es primordial para el análisis de aceleración.
Pero, ¿Cuál es la estrategia a utilizar para resolver el problema de velocidad en mecanismos planos?. Pues bien, lo primero a considerar es que para realizar el análisis de velocidad, se debe disponer de una ecuación de velocidad la cual se obtendrá al derivar la ecuación de posición con respecto al tiempo; si la ecuación de posición es algebraica, entonces la ecuación de velocidad será algebraica con una sola incógnita; pero si la ecuación de posición es vectorial, entonces se tendrá una ecuación de velocidad vectorial con dos incógnitas, pero que puede ser resuelta por medio de la descomposición rectangular.
La estrategia para resolver el problema de velocidad en forma vectorial consiste en hacer una deducción de las ecuaciones de velocidad relacionando un punto de análisis con sus enlaces; mientras que si se trata de resolver el problema usando la ecuación algebraica, entonces simplemente se deriva la ecuación algebraica de posición.
Alternamente, existe una combinación de ambas estrategias que consiste en establecer las ecuaciones de restricción, separando la ecuación vectorial en componentes rectangulares, posteriormente, se deriva con respecto al tiempo cada una de las ecuaciones escalares obtenidas en la descomposición de las ecuaciones escalares .
Un comentario final e importante aclarar es, que mientras la posición de un mecanismo articulado puede tener dos soluciones alternas, en el análisis de velocidad se tendrá solo una solución para cada dato y posición de entrada. Esto se debe que al derivar la ecuación de posición se reduce el grado de la ecuación.
A continuación se presenta las bases matemáticas para comprender la naturaleza matemática del análisis de velocidad en mecanismos.
Defina el vector posición de la siguiente manera (ver más detalle en el apartado de Conceptos Cinemáticos):
$$\overrightarrow{r}=r\overrightarrow{\lambda }_\theta$$
donde
$${\overrightarrow{\lambda}_\theta} =cos\theta \hat{\imath}+sen\theta \hat{\jmath}$$
además se tiene que:
$${\overrightarrow{\lambda}_\theta}'=\partial\overrightarrow{\lambda}_\theta/\partial \theta =-sen\theta \hat{\imath}+cos\theta \hat{\jmath}$$
Movimiento de rotación.
Cuando una partícula se mueve alrededor de un punto con movimiento de rotación, entonces la magnitud de su posición no cambia con respecto al tiempo, pero la dirección si cambia, es por eso que para obtener la ecuación de velocidad se deriva con respeto al tiempo solamente el vector direccionador, es decir:
$$\overrightarrow{V}= \frac{d\overrightarrow{r}}{dt} =r\frac{\partial }{\partial \theta }\overrightarrow{\lambda }'_\theta\frac{d\theta}{dt}$$
donde $\omega$ es la velocidad angular en rad/seg, entonces la velocidad lineal de una partícula en rotación conocida como velocidad tangencial VT se define como $V^{T} = \omega r$, por lo tanto;
$$\overrightarrow{V}=V^{T}{\overrightarrow{\lambda}_\theta }'$$
Nota
La velocidad lineal de una partícula que se encuentra en rotación alrededor de un punto, se le conoce como velocidad tangencial, cuya magnitud es $V^{T} = \omega r$ y la dirección según denota ${\overrightarrow{\lambda _\theta}}'$, es perpendicular al radio de giro en el sentido a donde se dirige el sentido de la velocidad angular.
La nota 2 se puede ejemplificar mediante un gráfico mostrado en la Figura 2
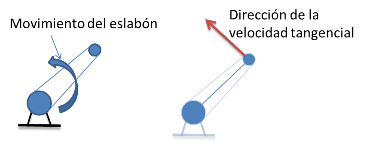
Figura 2. Dirección de la velocidad tangencial.
Movimiento de traslación rectilínea.
Cuando una partícula se mueve en línea recta, como las partículas de una corredera, entonces la componente vectorial que produce cambio es la magnitud, no así la dirección que permanece constante; por lo tanto, la velocidad del movimiento de rotación queda expresada como:
$$\overrightarrow{V}=V^L\overrightarrow{\lambda _\theta}$$
La ecuación anterior establece que cualquier partícula de un elemento con movimiento rectilíneo tiene una velocidad llamada velocidad rectilínea o lineal VT cuya magnitud es un dato proporcionado o desconocido, es decir, no se puede obtener por medio de una formula, el vector direccionador nos indica que dicha velocidad es paralela a la línea del deslizamiento tal y como se muestra en la Figura 3.
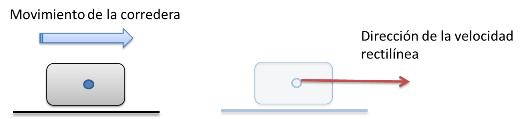
Figura 3. Dirección de la velocidad rectilínea
Nota 3
En un elemento con movimeinto de traslación rectilínea, todas las partículas de dicho elemento experimentarán la misma velocidad en magnitud y dirección conocida como velocidad rectilínea, cuya dirección es paralela a la línea de deslizamiento
Considere el sólido rígido y la representación vectorial de la posición de dos puntos cualesquiera P y Q como se muestra en la Figura 4
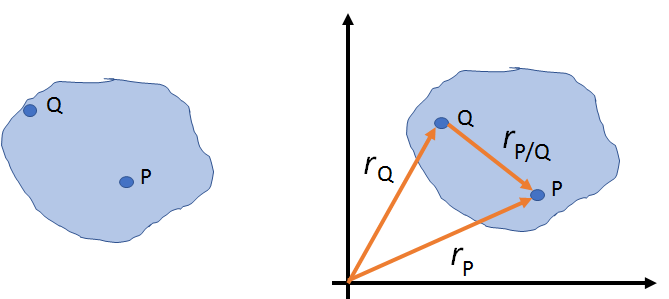
Figura 4. Movimiento plano general.
En la Figura 4 se puede apreciar dos vectores absolutos de posición $r_Q$ y $r_P$, mientras que el vector $r_{P/Q}$ se le conoce como vector relativo y denota la posición de P vista desde Q. La ecuación vectorial que relaciona estos tres vectores queda expresada como:
$$\overrightarrow{r}_P=\overrightarrow{r}_Q + \overrightarrow{r}_{P/Q}$$
NOTA
Se puede concluir que un cuerpo con movimiento plano general como el de la Figura 4, dos de cualesquiera de sus partículas pueden presentar cualquier tipo de movimiento, pero la trayectoria relativa de dos puntos de los mismos, como P vista desde Q, SIEMPRE es circular, ya que la distancia entre ellos permanece constante mientras la dirección entre ellos puede cambiar
Si se deriva la ecuación de posición de puntos de la misma barra con respecto al tiempo, entonces se tiene la ecuación de velocidad expresada como:
$$\overrightarrow{V}_P=\overrightarrow{V}_Q + \overrightarrow{V}_{P/Q}$$
Note como a la velocidad relativa P vista desde Q se le puede asignar SIEMPRE el término de velocidad tangencia, ya que como se explico en la NOTA 4, este vector de posición tiene un movimiento de rotación, por lo tanto:
$$\overrightarrow{V}_P=\overrightarrow{V}_Q + V^T_{P/Q}{\overrightarrow{\lambda _{P/Q}}}' $$
Existen algunos elementos como los collarines, los cuales están presentes en los mecanismo de deslizamiento, donde dicho elemento además de tener movimiento de traslación rectilínea, tine un movimiento de rotación alrededor de un punto. Para estos casos es notable que la velocidad total es la suma de la velocidad tangencial y la velocidad rectilínea, es decir
$$\overrightarrow{V} = V^T{\overrightarrow{\lambda _\theta}}' + V^L\overrightarrow{\lambda _\theta}$$
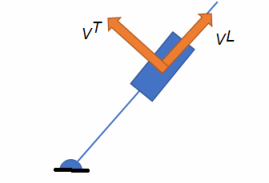
Figura 5. Dirección de velocidad con movimiento de rotación y traslación.
Created with the Personal Edition of HelpNDoc: Full-featured Documentation generator