Mecanismo manivela-corredera (RRRP)

Método algebraico para el análisis de posición de un mecanismo RRRP

El análisis de posición del mecanismo manivela-corredera se establecerá considerando a la manivela como elemento motriz y a la corredera como elemento de salida.

Para el análisis de posición se considera la siguiente nomenclatura.

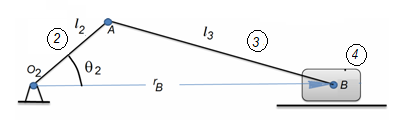
Figura 1. Mecanismo manivela-corredera o RRRP

1. Datos de la topología.

Para el análisis de posición del mecanismo de la Figura 1 se consideran los datos topológicos $l_{2}$, $l_{3}$ que son las longitudes de la manivela y la biela, respectivamente; además de la corredera se considera deslizandoce sobre una guía horizontal que pasa por el pivote O2.

2. Datos cinemáticos.

Como dato cinemático o dato de entrada considerar el ángulo de la manivela θ2, y como dato de salida el desplazamiento de la corredera (RB).

3. Objetivo.

Determinar una estrategia gráfica y/o analítica para determinar la posición de la barra de salida RB en función de la posición de la barra de entrada θ2  como se ejemplifica en la siguiente animación:

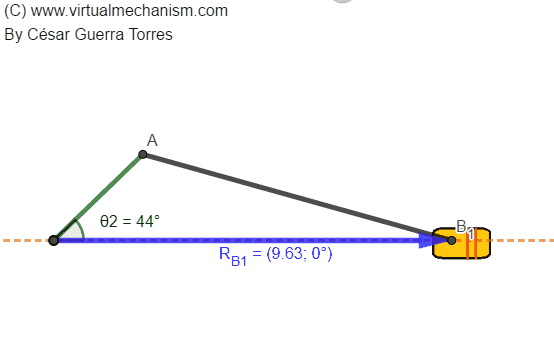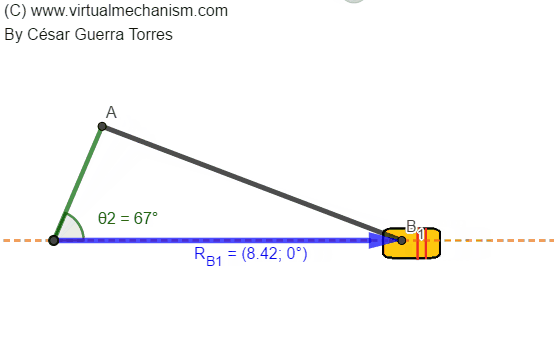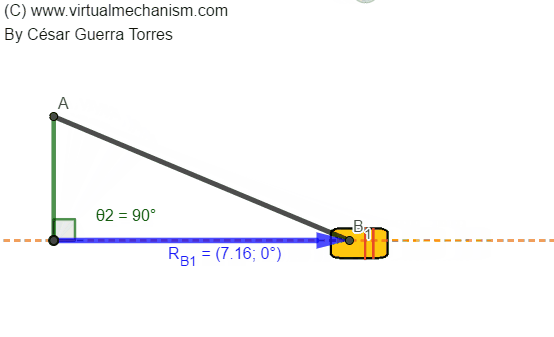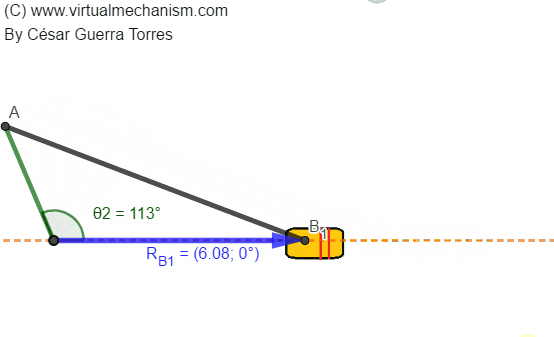
5. Análisis.

5.1 ECUACIONES VECTORIALES

Para el  método analítico el mecanismo, primero se debe expresar la posición de las articulaciones en forma vectorial tal como se muestra en la Figura 2.

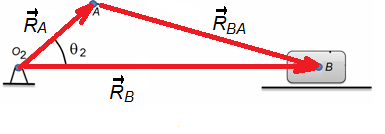
Figura 2. Expresión vectorial de posición en un mecanismo RRRP.

A partir de la figura 2, se puede definir la ecuación de posición de la siguiente manera:

$$\overrightarrow{R}_{B}=\overrightarrow{R}_{A}+\overrightarrow{R}_{BA}$$

La cual puede reescribirse en forma rectangular de la forma:

$$R_B\overrightarrow{\lambda} _{\theta B}=l_2\overrightarrow{\lambda} _{\theta 2}+l_3\overrightarrow{\lambda} _{\theta 3}$$

Donde $\overrightarrow{\lambda} _{\theta}=cos\theta\widehat{i}+sen\theta\widehat{j}$.

5.2 REDUCCIÓN A ECUACIÓN ALGEBRAICA

Si $\theta_2$ es el dato de entrada y $R_B$ el de salida, entonces se requiere eliminar $\theta_3$ mediante un artificio gráfico, este consiste en despejar $l_3\overrightarrow{\lambda} _{\theta 3}$  y multiplicarlo por si mismo, ya que $\overrightarrow{\lambda} _{\theta}\overrightarrow{\lambda} _{\theta}=1$, además $\overrightarrow{\lambda}_{\theta B}\overrightarrow{\lambda}_{\theta A}=cos(\theta_B-\theta_A)$, por lo tanto:

$$l_3\overrightarrow{\lambda}_{\theta 3}=R_B\overrightarrow{\lambda} _{\theta B}-l_2\overrightarrow{\lambda} _{\theta 2}$$

$$l_3\overrightarrow{\lambda}_{\theta 3}\cdot l_3\overrightarrow{\lambda} _{\theta 3} =(R_B\overrightarrow{\lambda} _{\theta B}-l_2\overrightarrow{\lambda} _{\theta 2})\cdot(R_B\overrightarrow{\lambda} _{\theta B}-l_2\overrightarrow{\lambda} _{\theta 2}) $$

La cual, después de operaciones algebraicas y para el caso en que θB=0, entonces se tiene la siguiene expresión cuadratica que relaciona $R_B$ en función de $\theta 2$:

Ejemplo. Determine analiticamente la posición de la corredera para l2 = 3 cm, l3 = 7 cm y  θ2. =  60o

Con estos datos se puede obtener de la ecuación (Ec1) como resultado RB2 - 3RB,-40 = 0, la cual al ser una ecuación cuadrática se puede resolver usando la fórmula general.  como resultado se tiene que:

RB1 = 8 cm, y RB2 = -5 cm

y que se puede demostrar en la gráfica 1 del ejemplo 1 usando métodos gráficos.

Como puede apreciarse, se tienen dos resultados y ambos son correctos en el sentido cinemático, ya que como puede corroborarse en la gráfica 1 del ejemplo 1, la circunferencia corta en la línea de deslizamiento en dos puntos y corresponden a las dos soluciones del mecanismo, por lo general suele llamarse solución abierta y cerrada, respectivamente.

Para demostración computacional pulse aquí

Created with the Personal Edition of HelpNDoc: Easy EPub and documentation editor