Método algebraico para el análisis de posición de un mecanismo RRRR
El análisis de posición del mecanismo manivela-corredera se establecerá considerando a la manivela como elemento motriz y a la corredera como elemento de salida.
El análisis de posición del mecanismo manivela-corredera consiste en establecer una ecuación que relacione la posición de la corredera en función de la posición angular de la manivela.
Para el análisis de posición se considera la siguiente nomenclatura:
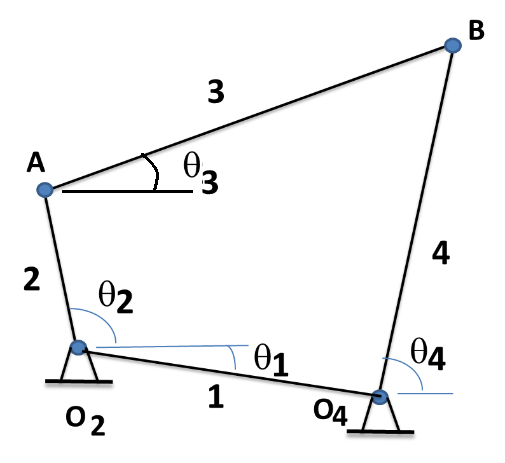
Figura 1. Mecanismo de cuatro barras o RRRR
Datos de la topología
Considere l2, l3 y l4 como las longitudes de los eslabones 2,3 y 4, respectivamente, mientras que l1 denota la distancia de pivote a pivote. Por su parte θ1 denota el ángulo entre pivote a pivote el cuál si se mide en contra de las manecillas del reloj, se medirá con signo negativo.
Datos cinemáticos.
θ2 y θ4 denotan las coordenadas de posición de la barra 2 y la barra 4, respectivamente.
Objetivo.
Determinar una estrategia gráfica y/o analítica para determinar la posición de la barra de salida θ4 en función de la posiciíon de la barra de entrada θ2.
Análisis.
ECUACIONES VECTORIALES
Considere los vectores de posición como se muestra en la Figura 2.
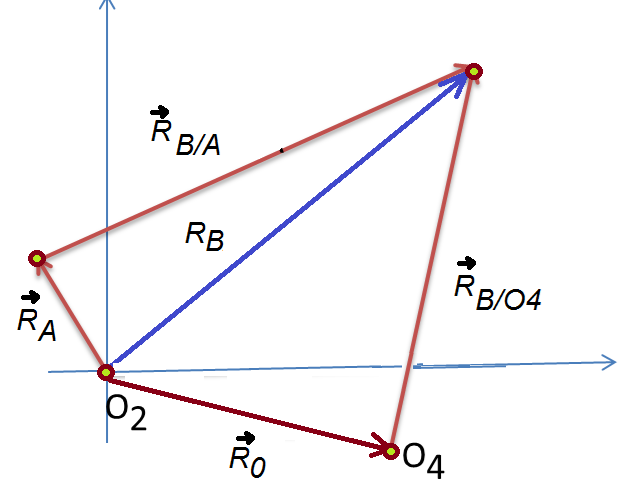
Figura 2. Diagrama vectorial de posición
La ecuación vectorial que define la restricción cinemática es:
$$\overrightarrow{R}_{B} = \overrightarrow{R}_{A}+\overrightarrow{R}_{B/A}$$
$$ \overrightarrow{R}_{B} = \overrightarrow{R}_{O_{2}}+\overrightarrow{R}_{B/O_{4}}$$
Igualando las ecuaciones anteriores se puede obtener una ecuación vectorial, de modo que disponiendo de los datos de la topologia del mecanismo, se tiene como incógnita θ3 y θ4 ya que θ2 es el dato cinemático de entrada.
$$\overrightarrow{R}_{O_{2}}+\overrightarrow{R}_{B/O_{4}}= \overrightarrow{R}_{A}+\overrightarrow{R}_{B/A}$$
REDUCCIÓN A ECUACIÓN ALGEBRAICA
Cada vector puede expresarse en su magnitud y dirección como: $ \overrightarrow{R}_{A} = l_{2}\angle\theta _{2}$, $ \overrightarrow{R}_{B/A} = l_{3}\angle\theta _{3}$, $ \overrightarrow{R}_{O_{2}} = l_{1}\angle\theta _{1}$ y $ \overrightarrow{R}_{B/O_{4}} = l_{4}\angle\theta _{4}$.
Para la reducción a una ecuación algebraica, es necesario eliminar una de las incógnitas, como lo más común es expresar el ángulo de salida θ4 en función del ángulo de entrada θ2, se procede a eliminar θ3 despejando el vector $\overrightarrow{R}_{B/A}$
$$\overrightarrow{R}_{B/A}=\overrightarrow{R}_{O_{2}}+\overrightarrow{R}_{B/O_{4}}- \overrightarrow{R}_{A}$$
Multiplicando ambos miembros de la ecuación por sí mismo usando el producto escalar, agrupando términos se tiene la ecuación final de posición conocida como ECUACION DE FREUDESTEINT.
$$k_{1}-k_{2}cos(\theta_{4}-\theta_{1})+k_{3}cos(\theta_{2}-\theta_{1})+cos(\theta_{4}-\theta_{2})=0$$ |
Ec1. Ecuación de Freudestein |
donde:
$k_{1}=\frac{{l_{3}}^{2}-{l_{1}}^{2}-{l_{2}}^{2}-{l_{4}}^{2}}{2l_{2}l_{4}}$, $k_{2}=\frac{l_{1}}{l_{2}}$, $k_{3}=\frac{l_{1}}{l_{4}}$ |
Ec 2 Constantes K |
La ecuación (1) estable la relación entre la coordenada de salida (θ4) vs. la coordenada de entrada (θ2) pero resulta complicado despejar dicha variable ya que se tendría que usar propiedades trigonométricas.
Alternativamente existe una solución si primero se hace primero un cambio de coordenadas en la ecuación (1) usando: $\theta_{4}' = \theta_{4}-\theta_{1}$ y $\theta_{2}' = \theta_{2}-\theta_{1}$, posteriormente usando propiedades trigonométricas, se tiene
$$Acos(\theta_{4}')+Bsen(\theta_{4}') = C$$ |
Ec 3. |
donde:
$$A=2l_{2}l_{4}cos(\theta_{2}')-2l_{1}l_{4}$$ $$B=2l_{2}l_{4}sen(\theta_{2}')$$ $$C={l_{1}}^{2} -{l_{2}}^{2} -{l_{4}}^{2} - 2l_{1}l_{2}cos(\theta_{2}')$$ |
Ec 4. |
La solución de la ecuación (3) es:
$$\theta_{4}' = tan^{-1}\left ( \frac{B}{A} \right )\pm cos^{-1}\left ( \frac{C}{\sqrt{A^2+B^2}} \right )$$ |
Ec 5 |
NOTAS de la Ec 5.
Created with the Personal Edition of HelpNDoc: Free EPub producer