Grado de libertad

El grado de libertad (GDL)´en mecanismos  es un parámetro que permite determinar el número de entradas de posición, las cuales permitan definir todas las posiciones del mecanismos. Así un mecanismo de 1 GDL requiere de una entrada para determinar todas las posiciones del mecanismo, uno de 2 GDL de dos entradas, y así sucesivamente.

Por ejemplo, en la Figura 1, se muestran dos mecanismos de 3 eslabones mas el fijo cada uno; el primer eslabonamiento esta articulado en sus extremos teniendo así  solo 1 GDL, por lo que requiere de solo un motor de entrada para mover todo el mecanismo; mientras tanto si se elimina una articulación, por ejemplo la del lado derecho, entonces se transforma en un mecanismo de 3 GDL y requiere de 3 motores para mover los tres eslabones.

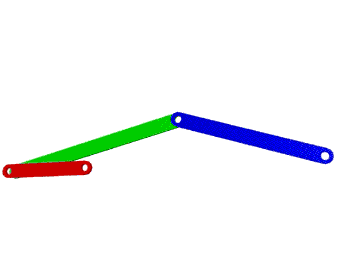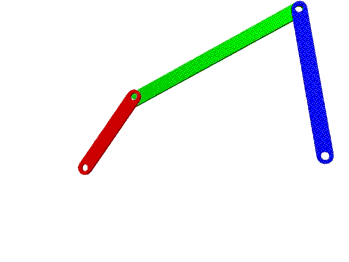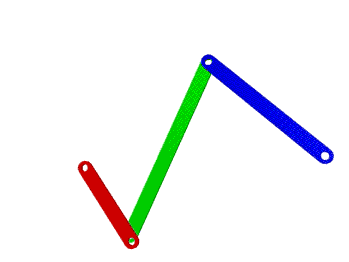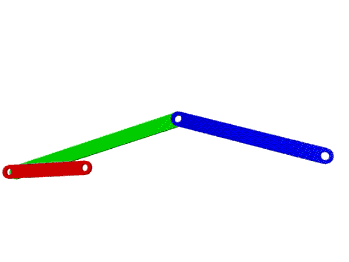
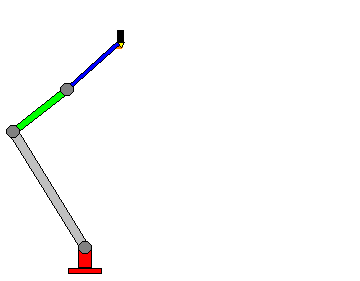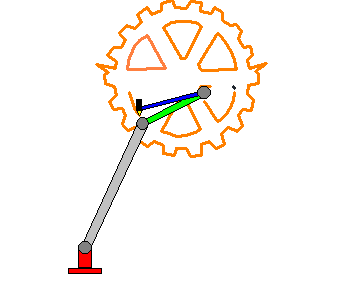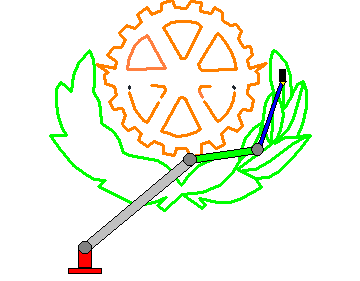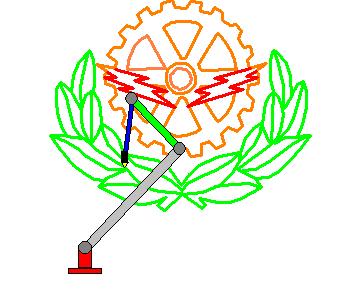
Figura 1. Mecanismo de 4 eslabones de 1GDL (a) y 3 (GDL)

Es evidente que entre más grados de libertad se tenga en un eslabonamiento, se puede realizar tareas más complejas que las de un solo grado de libertad.

Para obtener el grado de libertad en un eslabonamiento se puede utilizar la siguiente expresión:

GDL = 3(N-1) - 2J -K                                (Ec1)

donde N: número de eslabones incluyendo el elemento fijo, J: denota el número de juntas de 2 restricciones como las revolutas o prismáticas por cada par de eslabones unidos; por último,  K: denota el número de juntas de 1 restricción como patines o contacto superficial por cada par de eslabones unidos.

La ecuación Ec1 se puede interpretar de la siguiente manera: el número 3 indica que un sólido tiene 3 movimientos INDEPENDIENTES en un plano, que son traslación en el eje X, traslación en el eje Y y la rotación, es decir, es de  3 GDL.

Ahora se procede a restringir los GDL según las juntas cinemáticas. El número 2 de la ecuación hace referencia aquellas juntas que restringen la movilidad de un sólido rígido en DOS. como se muestra en la Figura 2, una revoluta limita el movimiento a la rotación, eliminando la movilidad en ejeX y ejeY ( 2 restricciones), de manera similar, una corredera solo permite el movimiento de traslación rectilínea.

Figura 2. Elementos con 2 restricciones.

Por su parte, los elementos de 1 restricción se pueden presentar en guías o patines, así como en elementos de contacto superficial como se muestra en la Figura 3.

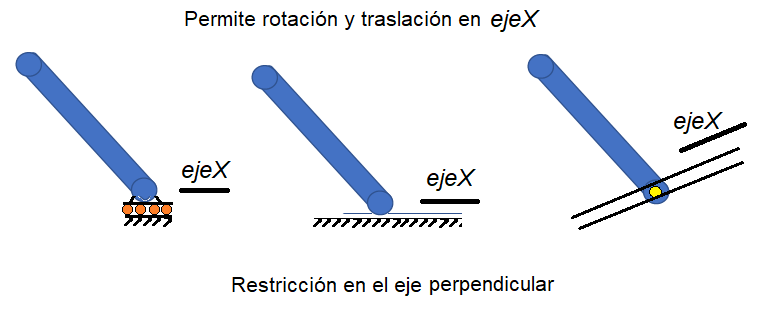
Figura 3. Elementos de 1 restricción.

Por lo tanto, la ecuación EC1 sugiere que se debe determinar el número de eslabones y luego restarle las restricciones según sus juntas cinemáticas y así determinar finalmente el GDL del eslabonamiento.

Ejemplo.

Considere  los mecanismos de la Figura 4, determine el GDL de cada uno de ellos.

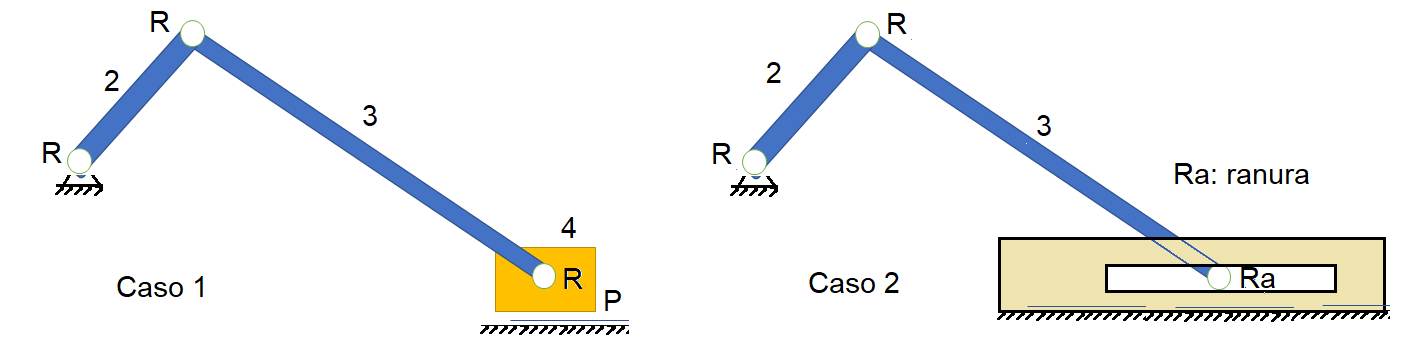
Figura 4. Dos representaciones de un mecanismo manivela-corredera.

Aún cuando ambos mecanismo pueden referenciar a un mecanismo manivela corredera, la verdad que tienen diferentes elementos y puede confundirse sobre todo en el cálculo del GDL

Caso 1: N = 4, J = 4 (3R + 1P), K = 0 , por lo tanto GDL = 3(4-1) - 2(4) -0 = 1 GDL

Caso 2: N = 3: J=3 (3R) , K =1 (Ra), por lo tanto GDL = 3(3-1) -2(3) - 1 = 1 GDL

Un caso conveniente a estudiar se presenta cuando en un eje se pueden tener varias revolutas que unen par de eslabones como se muestra en la Figura 5

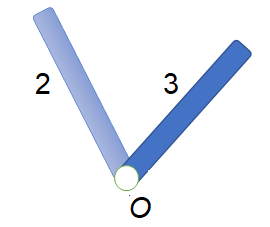
Figura 5. Dos casos posibles en un eje con varias revolutas.

Si el eje O tiene dos revolutas independientes, una para el elemento fijo y 2 y otra para el elemento fijo y 3, entonces se tendrá 2 GDL, es decir N  = 3 (Fijo, 2 y 3) , J= 2, K =0, entonces GDL = 3(3-1) - 2(2) = 2 GDL.

Pero si en el eje O, se tiene una sola revoluta, entonces es poruq en realidad 2 y 3 forman un solo eslabón, por lo tanto N = 2 (Fijo y ambos eslabones forman 1 solo elemento), J = 1, K =0, GDL = 3(2-1) - 2(1) - 0 = 1 GDL, lo cual resulta obvio que se requiera un solo elemento motriz para mover ambos eslabones ya que están unidos a la misma revoluta.

Ejemplo

Demuestre mediante la ecuación EC1, que el eslabonamiento de la Figura 6 es una estructura y no un mecanismo.

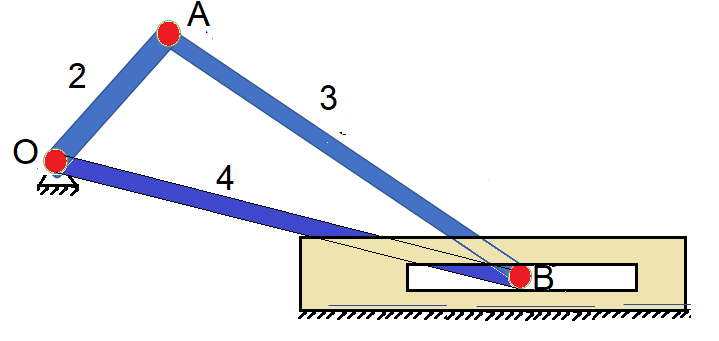
Figura 6. Ejemplo de una estructura

En el nodo O, se unen tres eslabones, el fijo el 2 y 4, por lo que se debe tener 2 revolutas 1.2 y 1,4 o bien pudiera ser 1,2 y 2.4, en A se tiene una revoluta, en B se tiene primero una revoluta que une a 3 y 4, los cuales terminan en una deslizadera de ranura.

en resumen, N = 4, K = 4, J = 1, por lo tanto

GDL = 3(4-1) -2(4)  - 1 = 0 GDL

Como es de 0 GDL, entonces no tiene movilidad, es una estructura.

Created with the Personal Edition of HelpNDoc: Easily create PDF Help documents