Guiado de sólido en dos posiciones: RRRR con rotopolos móviles

1. Introducción

En el apartado anterior se detalla un procedimiento para sintetizar la topología de una manivela que permita desplazar un objeto en dos posiciones prescritas, para ello se requiere de la intersección de dos mediatices. Pero resulta que pueden darse casos donde dicha intersección queda en un punto fuera del área de trabajo, lo que resulta imposible usar esta solución.

Para solucionar el problema anterior, en lugar de intersectar las mediatrices se puede localizar sobre cada una de ellas un rotopolo arbitrario y formar así un mecanismo doble oscilador como se muestra en la Figura 1.

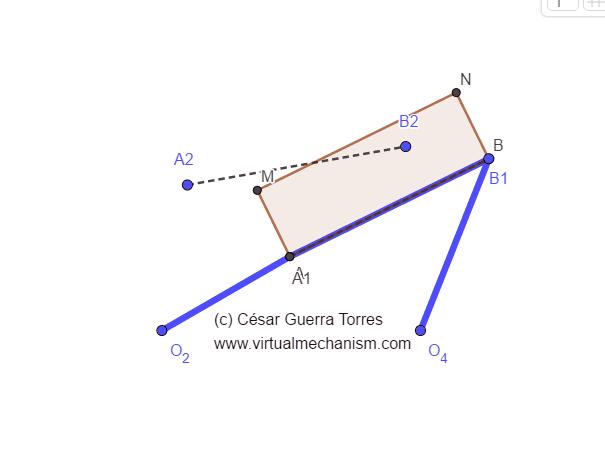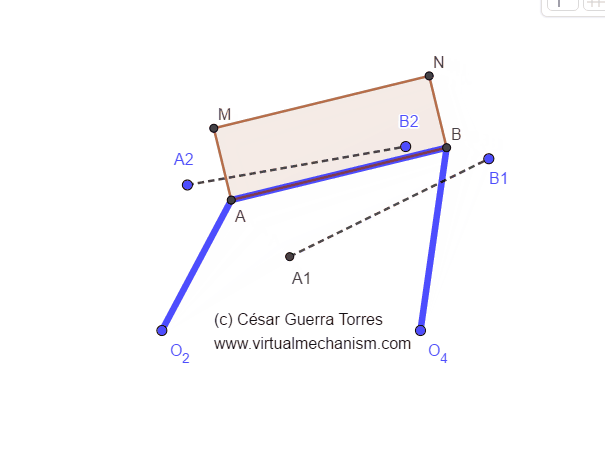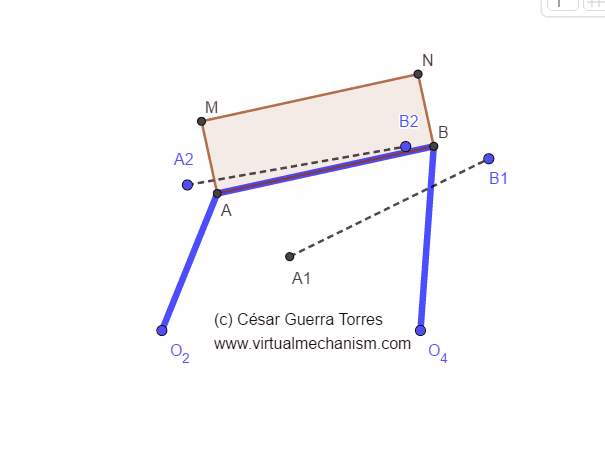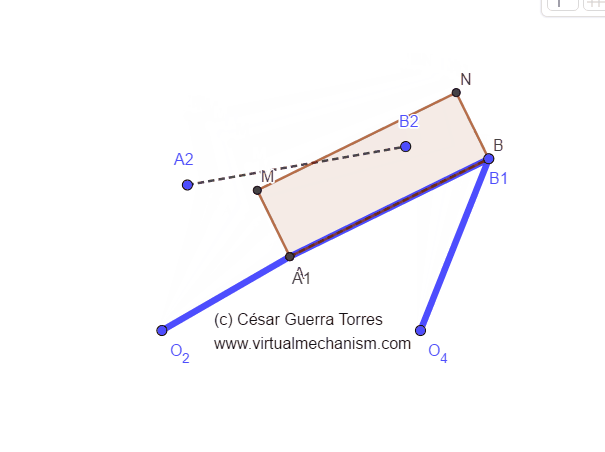
Figura 1. Mecanismo doble oscilador para la síntesis de guiado en dos posiciones.

Síntesis

Necesidad: Se desea desplazar un objeto en dos posiciones sobre un soporte, del soporte se extrae una línea de trabajo AB. Determine la topología de un mecanismo doble oscilador que permita desplazar el objeto en ambas posiciones A1B1 y A2B2 usando la biela como elemento de soporte.

Requerimiento para la síntesis. Datos relacionado con las dos posiciones deseadas del sólido rígido como son: longitud de la línea de trabajo (LAB) menor o mayor a la pieza a desplazar, datos vectoriales de las dos posiciones deseadas.

Resultado: El resultado de la presente síntesis se deberá tener los siguientes parámetros, mismos que se muestran en la Figura 2.

Tabla 1. Tabla de resultados

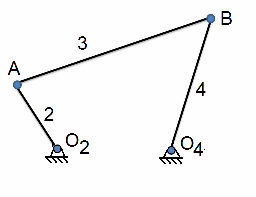
Figura 2.

2. Procedimiento

Método gráfico:

1. Definir línea de trabajo AB de longitud LAB.
2. Trazar en un plano cartesiano dos líneas de longitud similar LAB que denoten las posiciones deseadas de movimiento A1B2 y A2B2
3. Trazar dos rectas, una es la mediatriz entre los puntos A1A2 que se denotará como M1 y otra es la mediatriz entre B1B2 que se denotará como M2.
4. Sobre la recta M1 seleccionar un punto arbitrario que corresponderá con el pivote O2 y sobre la recta M2 otro que corresponderá con el pivote O4.
5. LLenar tabla de resultados usando la Figura 2.

Ejemplo:

Para comprender el procedimiento de construcción de un doble oscilador para desplazar un objeto en dos posiciones, considere el mismo ejemplo del apartado anterior:

 LAB =  6 cm

Tabla 2. Datos de diseño

De la tabla anterior es posible dibujar las dos líneas de trabajo, simplemente se trazan el punto A1 (2,0) y A2 (3,3.5); posteriormente los puntos B1 y B2 se trazan con los ángulos respectivos y con un segmento de LAB =  6 , es decir, B1 se traza a partir de A1 formando un ángulo de 20o con respecto al EjeX, B2 se traza de manera similar.

Posteriormente se trazan las mediatriz de A1A2 y de B1B2, sobre la cual se va a seleccionar ARBITRARIAMENTE los rotopolos O2 y O4, es decir, los pivotes de los osciladores.

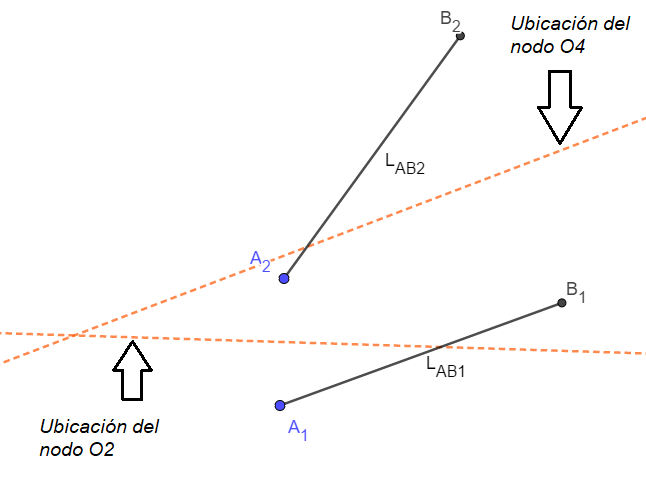
Figura 3. Procedimiento de síntesis RRRR para dos posiciones.

La Figura 3 muestra una selección arbitraria de los nodos O2 y O4, que son los pivotes, además muestra las dos posiciones del mecanismo deseadas.

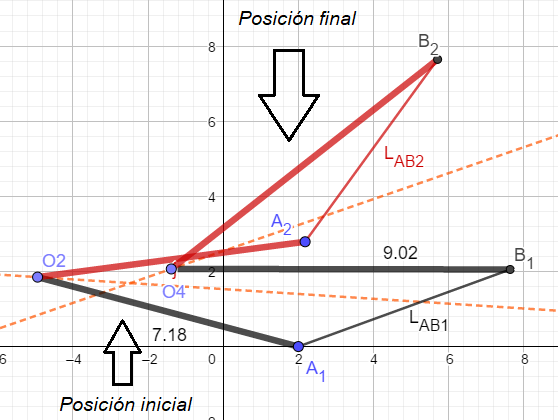
Figura 4. Resultado de la síntesis

Por lo tanto, el resultado de la síntesis de la gráfica de la Figura 4 arroja los siguientes valores

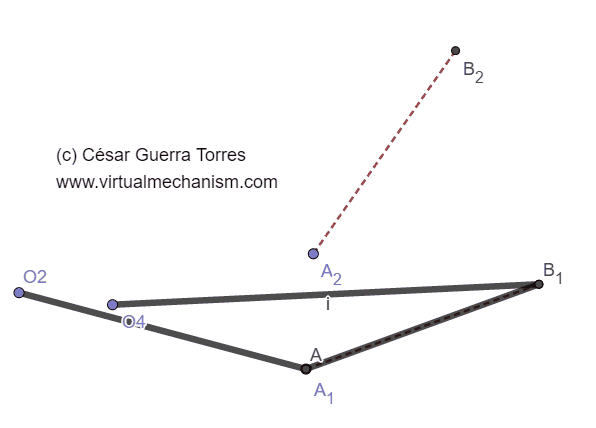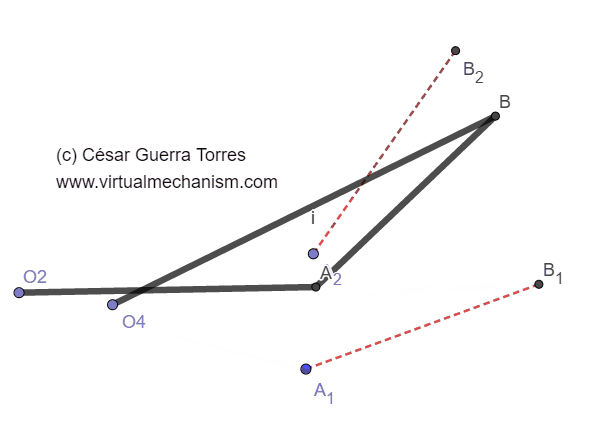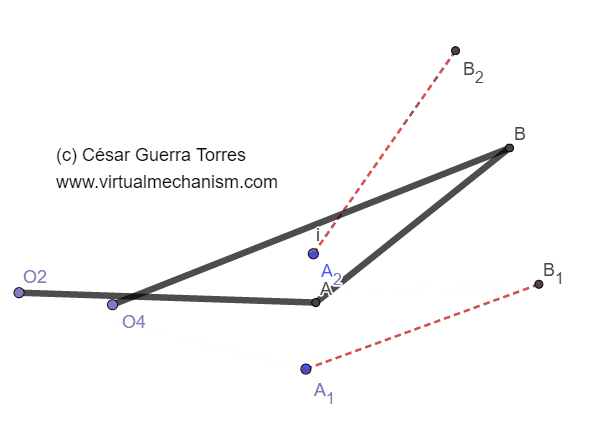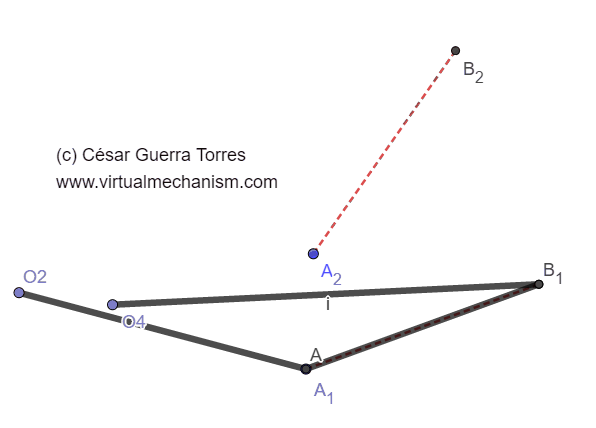
Figura 5. Animación del mecanismo resultado de la síntesis

NOTA

Es de importancia aclarar que la selección arbitraria de los rotopolos puede repercutir en el funcionamiento del mecnismo doble oscilador, es decir, aún cuando no se requiera en el mecanismo la condición de Grashof, debe cumplir con las condiciones de movilidad por lo menos en el rango de oscilación entre ambas posiciones. Pues bien, puede que en una selección de los rotopolos repercuta en la falta de movilidad entre las posiciones deseadas, la cual se puede solucionar moviendo nuevamente los rotopolos.

Otro problema que se puede presentar en la selección de los rotopolos, radica en el hecho de que éste tipo de mecanismos presenta dos soluciones para una misma entrada, llamadas solución cerrada y abierta; por lo tanto, puede que una posición corresponda a una solución y la otra posición pertenezca a la otra solución, por lo que aún cuando el mecanismo continúe su trayectoria sin enmarañarse, puede que una de las dos posiciones no corresponda a la deseada. De igual manera puede corregirse  re ubicando los rotopolos.

La Figura 6 muestra el problema de doble solución donde se ha re ubicado el rotopolo O4. Se muestra los dos mecanismos para una misma entrada O2A,  mientras que una solución formada por O2-A-B-O4 cumple con la posición deseada A1B1, no cumple para la posición A2B2, mientras que la solución O2-A-C-O4 (verde) cumple para el caso inverso.

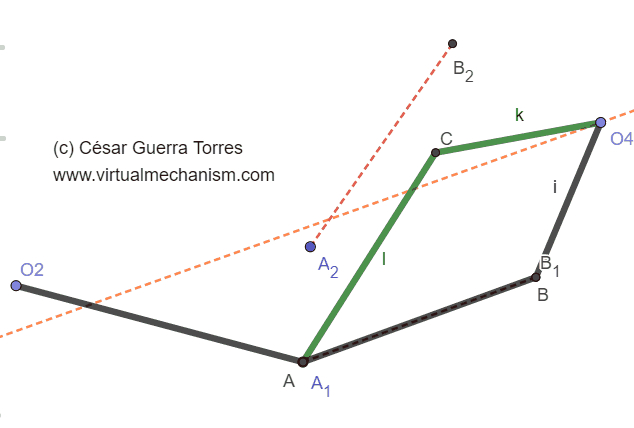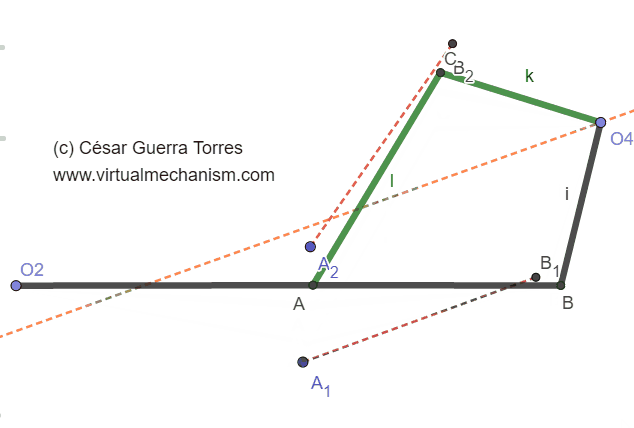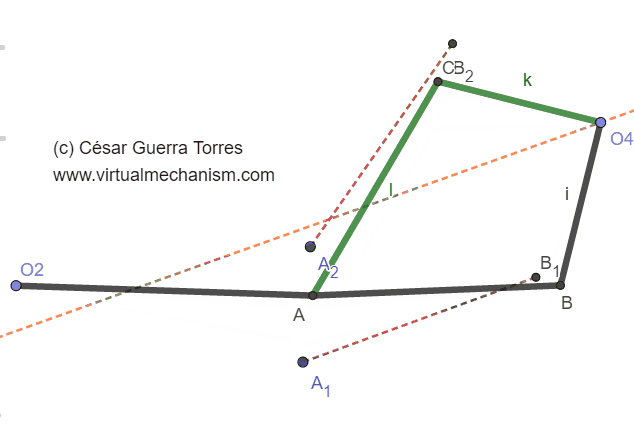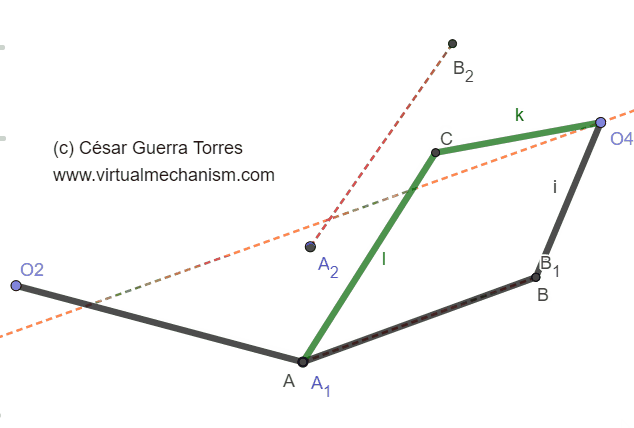
Figura 6. Problema de las dos soluciones.

2.2 Método analítico.

2.3 MWS

Created with the Personal Edition of HelpNDoc: Easy to use tool to create HTML Help files and Help web sites