Mecanismo manivela-corredera(RRRP)

Mathedemo

Método algebraico para analisis de velocidad de un mecanismo RRRP

Considere el mecanismo de la Figura 1

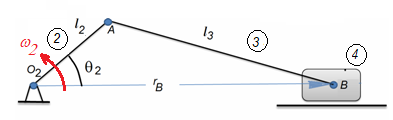
Figura 1. Mecanismo manivela-corredera o RRRP

Cuya ecuación algebraica de posición que relaciona la coordenada $R_B$ con $/tetha_2$ es:

$$P(R_B,\theta_2) = R_B^{2}-2R_Bl_2cos(\theta _2)+(l_2^{2}-l_3^{2})=0$$

Por lo tanto, si $V_B$ denota la velocidad de la corredera y $\omega_2$ la velocidad angular de la manivela 2, entonces la ecuación de velocidad se obtendrá:

$$V(V_B,\omega_2)=\frac{\partial}{\partial R_B}P(R_B,\theta_2)V_B + \frac{\partial}{\partial \theta_2}P(R_B,\theta_2)\omega_2=0$$

Por lo tanto

$$V(V_B,\omega_2)=(2R_B-2l_2cos(\theta_2))V_B+2R_Bl_2sen\left ( \theta_2 \right )\omega_2=0$$

despejando la velocidad de la corredera $V_B$ en función de la velocidad angular de la manivela $\omega_2$, se tiene:

$$V_B=\frac{-2R_Bl_2sen\left ( \theta_2 \right ) }{2R_B-2l_2cos(\theta_2)}\omega_2$$

Ec 1

Ecuación de velocidad RRRP

Como puede apreciarse y era de esperar, la velocidad de la corredera no solo depende de la velocidad angular de la manivela y los datos de topologia, si no de las coordenadas de posición, por lo que es necesario primero resolver el problema de posición.

Ejemplo 1.

Considere el mecanismo de la Figura 1 cuyas longitudes de los eslabones son $l_2=3 cm$, $l_3 = 7 cm$, usando el método de diferenciación finita, determine la velocidad promedio de la corredera cuando $\theta_2 = 40^o$ y $\omega_2=5 rad/seg$.

Solución:

Para usar la ecuación (1) se requiere la posición de la corredera cuando $\omega_2 = 5 rad/seg$. Para lograr lo anterior puede ser que se proporcione el diagrama cinemático con las longitudes y posiciones; en caso contrario se puede obtener usando cualquier método para el análisis de posición, o bien puede usar la herramienta MWS para determinar la posición.

Usando la herramienta MWS se tiene que para $\theta_2 = 40^o$, $R_B = 9.03 cm), por lo tanto

$$v_B=\frac{-2\times 9.03\times 3\times sen(40^o)}{2\times 9.0-23\times cos(40^o)}\times 5 = -12.93 cm/s$$

-------------------------------------------

$$v_B=-12.93 cm/s$$

----------------------------------------

Note que se uso el signo positivo de la velocidad angular 2 porque en la Figura 1, el sentido es en contra de las manecillas del reloj.
Por lo anterior, el signo negativo de la velocidad B indica que va hacia la izquierda en el instante analizado.

Created with the Personal Edition of HelpNDoc: Easy EBook and documentation generator