Análisis de velocidad de un mecanismo RRRR usando ecuaciones de restricción
Gracias al Prof. Alonso Salazar por su aportación
En este apartado se hará uso de las ecuaciones de restricción para el análisis de velocidad de un mecanismo articulado de cuatro barras como el que se muestra en la Figura 1 usando ecuaciones de restricción.

Figura 1. Mecanismo RRRR.
Ejemplo 1.
Considere el mecanismo de la Figura 1 cuyas longitudes y posiciones angulares se proporcionan. Si el disco 2 se mueve a una velocidad angular $13.71$ rad/seg CMR, determine la velocidad angular del eslabón 3 y 4; así como la del centro de masa de la barra 3 suponiendo que es rígida y homogénea.
Solución.
Sea G el nodo del centro de masa de la barra 3, el cuál por las características proporcionadas, corresponde a su centro geométrico, es decir a la mitad de la barra; por lo tanto, para determinar la velocidad de dicho nodo $V_G$ primero se tiene que resolver la velocidad de la barra 3 y 4, ya que la posición del C, depende de la posición del nodo A y el nodo B.
Cálculo de velocidades angulares $\omega_3$ y $\omega_4$:
Para la solución de velocidad se requiere la solución al problema de posición, la cual se proporciona en la Figura 1. un diagrama vectorial de cierra o restricción se muestra en la Figura 2.
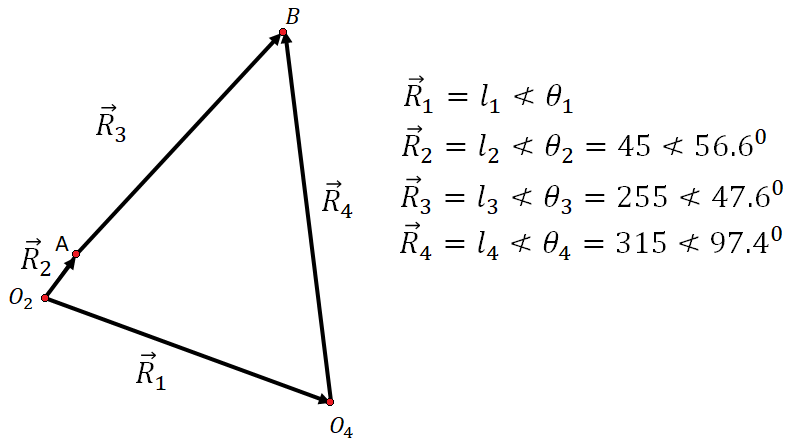
Figura 2. Diagrama vectorial del Ejemplo 1.
Del diagrama vectorial de la Figura 2, se tiene:
$$ \vec{R}_2 + \vec{R}_3 = \vec{R}_1 + \vec{R}_4$$
Y haciendo una descomposición rectangular:
$$\sum x:l_{2}cos\left (\theta_2 \right ) + l_{3}cos\left (\theta_3 \right )=l_{1}cos\left (\theta_1 \right )+l_{4}cos\left (\theta_4 \right )$$
$$\sum y:l_{2}sen\left (\theta_2 \right ) + l_{3}sen\left (\theta_3 \right )=l_{1}sen\left (\theta_1 \right )+l_{4}sen\left (\theta_4 \right )$$
Derivando con respecto al tiempo:
$$\sum x:-l_{2}\omega_2sen\left (\theta_2 \right ) -l_{3}\omega_3sen\left (\theta_3 \right )+l_{4}\omega_4sen\left (\theta_4 \right )=0$$
$$\sum y:l_{2}\omega_2cos\left (\theta_2 \right ) +l_{3}\omega_3cos\left (\theta_3 \right )-l_{4}\omega_4cos\left (\theta_4 \right )=0$$
Reemplazando los datos conocidos.
$$\sum x:-45(13.71)sen\left (56.6^o \right ) -255 \omega_{3}sen\left (47.2^o \right ) + 315\omega_{4}sen\left (97.4^o \right )=0 $$
$$\sum y:45(13.71)cos\left (56.6^o \right ) + 255 \omega_{3}cos\left (47.2^o \right ) - 315\omega_{4}cos\left (97.4^o \right )=0 $$
Cuyo resultado es:
------------------------------------------------------------------
$\omega_{3} = -2.05 rad/seg $ $\omega_{4} = 0.41 rad/seg$
------------------------------------------------------------------
Cálculo de la velocidad del nodo G:
Como se mencionó con anterioridad, el punto G depende de A y B, pero como se tiene el ángulo $\theta_3$ y la velocidad angular $\omega_3$, entonces podemos hacer una dependencia de la posición de $\vec{R}_A$ y de la posición $\vec{R}_{G/A}$ ya que el vector $\vec{R}_{G/A}$ depende de $\theta_3$ de la misma forma que $\vec{V}_{G/A}$ depende de la velocidad angular $\omega_3$.
Por lo tanto, para calcular la velocidad $V_G$ , se establece una ecuación de posición de cierre de $O_2$, A y G y quedará definida como:
$$\vec{R}_G = \vec{R}_A + \vec{R}_{G/A}$$
Como G depende de A y GA, entonces la solución de la posición de G $\vec{R}_G$ dependerá estrictamente de conocer completamente los vectores los vectores $\vec{R}_A$ y $\vec{R}_{G/A}$, es decir:
$$\vec{R}_G = l_2cos\left ( \theta_2 \right )\hat{\imath} + l_2sen\left ( \theta_2 \right )\hat{\jmath} + \frac{l_3}{2}cos\left ( \theta_3 \right )\hat{\imath} + \frac{l_3}{2}sen\left ( \theta_3 \right )\hat{\jmath}$$
Derivando la ecuación con respecto al tiempo:
$$\vec{V}_G = -l_2\omega_2sen\left ( \theta_2 \right )\hat{\imath} + l_2\omega_2cos\left ( \theta_2 \right )\hat{\jmath} - \frac{l_3}{2}\omega_3sen\left ( \theta_3 \right )\hat{\imath} + \frac{l_3}{2}\omega_3cos\left ( \theta_3 \right )\hat{\jmath}$$
Cuyo resultado es:
-------------------------------
$\vec{V}_G = -322\hat{\imath} + 163.3\hat{\jmath}$ cm/s
-------------------------------
Que en forma polar es:
-------------------------------
$\vec{V}_G = 130.35 \measuredangle 153.10^o$ cm/s
-------------------------------
Created with the Personal Edition of HelpNDoc: iPhone web sites made easy