Análisis gráfico de velocidad usando polígono

En este apartado anterior se planteo el procedimiento para resolver las ecuaciones vectoriales mediante un procedimiento analítico donde se relacionan nodos de interés o de velocidad desconocida, con nodos de velocidad conocida; en algunos casos era necesario asociar un mismo nodo de velocidad desconocida, con otros dos para poder buscar una solución.

La forma de solucionar dichas ecuaciones puede realizarse mediante trazos vectoriales, cuyo resultado gráfico se le conoce como polígono de velocidades, ya que son gráficas vectoriales de velocidad. Para aplicar esta metodología es necesario disponer del diagrama cinemático del mecanismo con sus medidas reales escaladas y en la posición de análisis, ya que los diagramas vectoriales se obtienen a partir del diagrama cinemático.

Procedimiento

1. Identifique el eslabón de velocidad conocida.
2. Establezca una ecuación vectorial que relacione dos puntos de dicho eslabón, calcule la velocidad de articulación $Q$ el cual continúa con la transmisión de movimiento hacia otros nodos.
3. Identifique un nodo de velocidad dependiente de $Q$ y que llamaremos $P$.
4. Identifique si el movimiento $P/Q$ es de rotación traslación y la combinación de ambos.
5. Establezca la ecuación, según sea el caso:

• P/Q es de rotación: $\vec{V}_P$ =  $\vec{V}_Q + \vec{V}^T_{P/Q}$ donde $\vec{V}^T_{P/Q}$ es una velocidad tangencial, es decir $v^T_{P/Q} =( \omega_{P/Q}) (r_{P/Q})$.
• P/Q es de traslación . $\vec{V}_P$ =  $\vec{V}_Q + \vec{V}^L_{P/Q}$ donde $\vec{V}^L_{P/Q}$  es la velocidad lineal de traslación.
• P/Q es de rotación y traslación. $\vec{V}_P$ =  $\vec{V}_Q + \vec{V}^T_{P/Q} +\vec{V}^L_{P/Q} $

6. La solución de la ecuación anterior puede ser analítica según se planteó en el apartado anterior, o bien gráfica como se sugiere a continuación:

• Se requiere a escala de diagrama cinemático del mecanismo.
• Plantear la ecuación a solucionar.
• Identificar el vector de velocidad conocida tanto en magnitud como en dirección.
• Coloca un punto que llamaremos Ov donde se graficará el polígono de velocidades.
• Dibujar el vector de velocidad conocida en dicho origen Ov, usando su magnitud y dirección (perpendicular o paralelo, según sea el caso) ver tabla 1
• CASO1: Si se desconocen la magnitud de los otros dos vectores de velocidad, trazar una linea que denote la dirección de los vectores, trazando un polígono sobre el vector conocido.
• CASO 2: Si se conoce completamente otro vector, por lo que se desconoce completamente el otro vector, trazar consecuentemente el vector conocido sobre el anterior y la resultante será el vector desconocido.

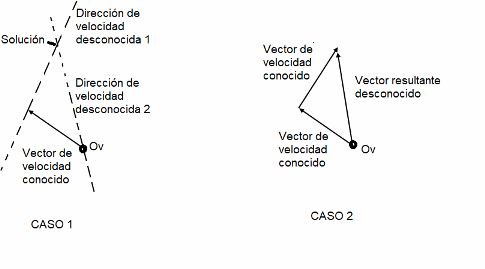
Figura 1. Solución gráfica al polígono vectorial

Ejemplos:

1. Mecanismo manivela-corredera

Created with the Personal Edition of HelpNDoc: Easily create EBooks