Mecanismo manivela-corredera (RRRP)

En este apartado se hará uso de la metodología expuesta en el apartado por diferenciación finita, para determinar la velocidad en un punto dado de un mecanismo manivela-corredera como el que se muestra en la Figura.1.

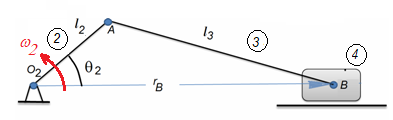
Figura 1. Mecanismo manivela-corredera o RRRP

Ejemplo 1.

Considere el mecanismo de la Figura 1 cuyas longitudes de los eslabones son $l_2=3 cm$, $l_3 = 7 cm$, usando el método de diferenciación finita, determine la velocidad promedio de la corredera cuando $\theta_2 = 40^o$ y $\omega_2=5 rad/seg$.

Solución:

Independientemente del método utilizado para el análisis de velocidad, se necesita primero solucionar el problema de posición del mecanismo para obtener todas las coordenadas de posición. Para lograr lo anterior puede ser que se proporcione el diagrama cinemático con las longitudes y posiciones; en caso contrario usar cualquiera de los métodos vistos con anterioridad

Análisis de la barra 2

Para  la solución usando el presente procedimiento, primero analizamos el nodo $A$ dependiendo del nodo $O_2$ ya que ambos dependen del eslabón 2 cuyo dato es conocido.

$$\vec{V}_A=\vec{V}_{O_2}+\vec{V}_{A/O_2}$$

como el nodo $O_2$ esta fijo, por lo tanto no tiene velocidad, ahora la ecuación se escribe como:

$$\vec{V}_A=\vec{V}_{A/O_2} = \omega_2 l_2\lambda'_{\theta_2}=(+5r/s)(3cm)[-sen(40^o)\hat{\imath}+cos(40^o)\hat{\jmath}]$$

--------------------------------------------------------------------------------------
$$\vec{V}_A=-9.64\hat{\imath}+11.49\hat{\jmath}$$

--------------------------------------------------------------------------------------

Análisis de la barra 3

Teniendo como dato la velocidad del nodo $A$, entonces se procede a determinar la velocidad del $B$ a partir de $A$, es decir

$$\vec{V}_B=\vec{V}_A+\vec{V}_{B/A}$$

De la ecuación anterior, la velocidad $V_A$ es completamente conocida, por su parte la velocidad $V_{B/A}$ se conoce su dirección ya que se sabe que tiene movimiento de rotación relativa. Por último, de la velocidad $V_B$ se puede decir que se conoce su dirección ya que se conoce su trayectoria, que es rectilínea, pero tal afirmación debe ser respaldada mediante una ecuación, es decir relacionar el Nodo B con el Nodo $0_2$, ya que B se desliza sobre una guía que pasa por $O_2$, es decir

$$\vec{V}_B=\vec{V}_{O_2}+\vec{V}_{B/O_2}$$

Como $\vec{V}_{O_2} = \vec{0}$. entonces $\vec{V}_B=\vec{V}_{B/O_2}$ quedando demostrado lo dicho con anterioridad. Este último procedimiento va a ser útil en el análisis de mecanismos con deslizamiento, de aquí la importancia de su explicación aunque parezca evidente.

Como de $V_B$ se conoce la dirección, deslizándose en la horizontal, más no su magnitud; de la $V_A$ se conoce todo, se acaba de obtener en un paso anterior, y además de la $V_{B/A}$ se conoce solo su dirección al tener movimiento de rotación, más no se conoce su magnitud; por lo tanto, se tienen dos incógnitas, lo que significa que la ecuación $\vec{V}_B=\vec{V}_A+\vec{V}_{B/A}$.

Usando la tabla 1 del apartado anterior, se escribe la ecuación como:

$$v_B\vec{\lambda}_{\theta _B}=v_A\vec{\lambda}_{\theta _2}' + v_{B/A}\vec{\lambda}_{\theta _3}'$$

Por definición se tiene: ${\overrightarrow{\lambda}_\theta} =cos\theta \hat{\imath}+sen\theta \hat{\jmath}$, mientras que su derivada es:  ${\overrightarrow{\lambda}_\theta}'=-sen\theta \hat{\imath}+cos\theta \hat{\jmath}$; además aplicando una descomposición rectangular a la última ecuación se tiene:

$$\Sigma v_x:v_Bcos(\theta_B)=v_{A_x}+(v_{B/A})(-sen(\theta_3))$$

$$\Sigma v_y:v_Bsen(\theta_B)=v_{A_y}+(v_{B/A})(cos(\theta_3))$$

Note que la velocidad $V_A$ se expresó en sus componentes x e y, ya que se obtuvieron en el paso anterior, es decir $v_{A_x} = -9.64\cm/s$, $v_{A_y} = 11.49 cm/s $, por su parte como dato se tiene $\theta_2 = 40^o$ y resolviendo el problema de posición o bien usando el MWS, se obtiene $\theta_3=-16^o $ , por lo tanto:

$$v_Bcos(0^o)=-9.64+v_{B/A}(-sen(-16^0))$$

$$v_Bsen(0^o)=11.49+v_{B/A}(cos(-16^0))$$

Solucionando el sistema de ecuaciones, se tiene

-------------------------------------------------------------------------

$v_B=-12.93 cm/s$     y   $v_{B/A}=-11.95 cm/s$      

----------------------------------------------------------------------

Como la velocidad $v_{B/A}$ es tangencial significa que $v_{B/A} = \omega _3 \times r_{B/A}$ , por lo tanto:

-----------------------------------------------------------

$\omega _3 =\frac{-11.95 cm/s}{7 cm} = -1.70 rad/seg$

-------------------------------------------------------------

Created with the Personal Edition of HelpNDoc: Easy CHM and documentation editor