Relación de tiempo

Relación de tiempo

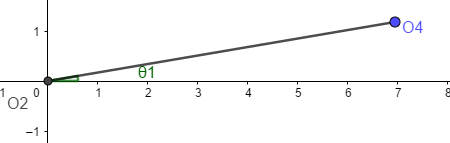
Considere el mecanismo manivela-oscilador de la Figura 1, donde las longitudes son L2,L3 y L4  son las longitudes de la manivela 2, biela 3, oscilador 4, respectivamente, mientras que L1  es la longitud desde O2 a O4 y  θ1 el ángulo en dichos pivotes.

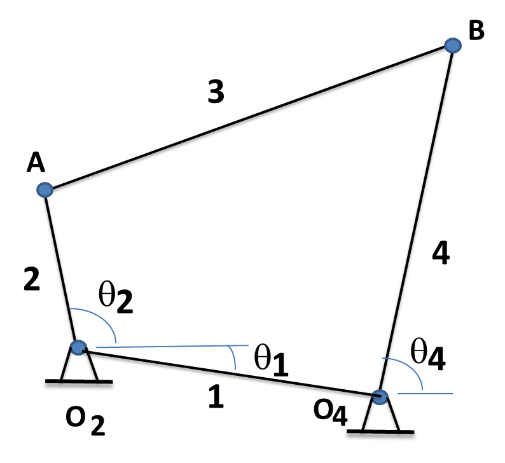
Figura 1. Mecanismo manivela-oscilador.

Se dice que el oscilador 4 tiene una relación de tiempo (Q) que se puede obtener como:

$$Q=\frac{t _{av}}{t _{ret}}$$

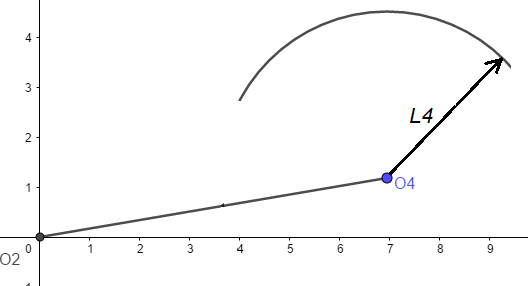
Donde $t_{av}$ es el tiempo de avance del oscilador y $t_{ret}$ el tiempo de retroceso tal como se muestra en la Figura 2.

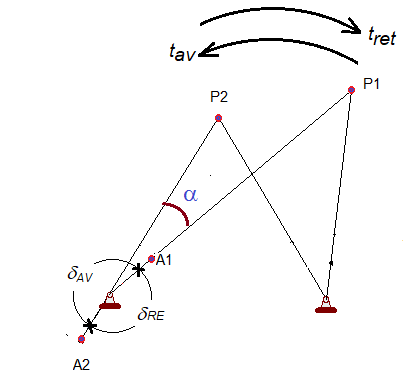
Figura 2. Parámetros que involucran la relación de tiempo Q.

Ya que el tiempo de avance y retroceso del oscilador dependen de las condiciones extremas o límites (topes) del oscilador, entonces es importante analizar todos los parámetros que definen las posiciones extremas. En la Figura 2, se puede apreciar que la relación de tiempo Q también esta asociada con los ángulos de avance y retroceso pero de la manivela, llamados ángulo de avance δAV y el ángulo de retroceso δRE.

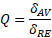         (Ec 1)

De la misma manera, es posible percibir en la Figura 2 que si :

       (Ec2)

Por lo tanto, la relación de tiempo también se puede calcular como:

        (Ec 3)

Pero para el análisis de la relación de tiempo Q, es necesario tomar en cuenta la topología del mecanismo, es decir las longitudes L1, L2, L3 y L4, así como el ángulo θ1. Para ello es necesario que para asegurar que el oscilador se encuentra en una posición extrema o límite de la oscilación, entonces la manivela 2 y la biela 3 deberán estar en posición paralela una con respecto a otra como se puede apreciar en la Figura 3.

Para el análisis de la relación de tiempo Q, es necesario tomar en cuenta la topología del mecanismo, es decir las longitudes L1, L2, L3 y L4, así como el ángulo θ1. Para ello es necesario que para asegurar que el oscilador se encuentra en una posición extrema o límite de la oscilación, entonces la manivela 2 y la biela 3 deberán estar en posición paralela una con respecto a otra como se puede apreciar en la Figura 3.

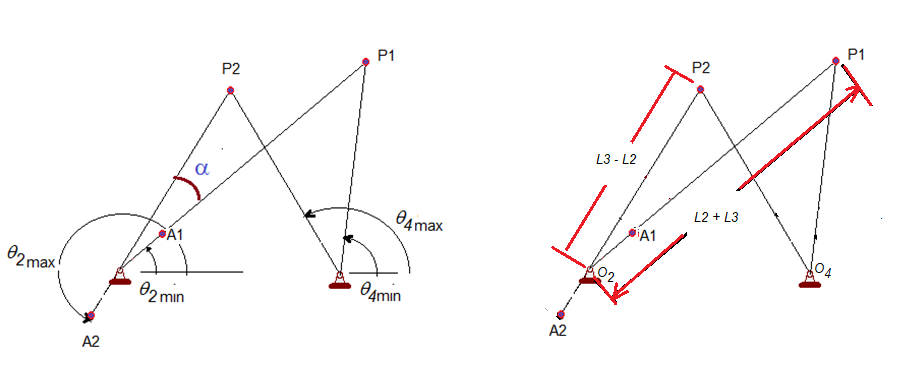
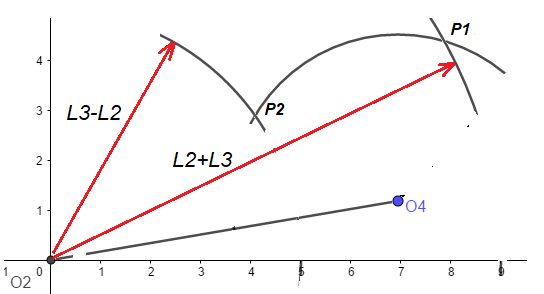
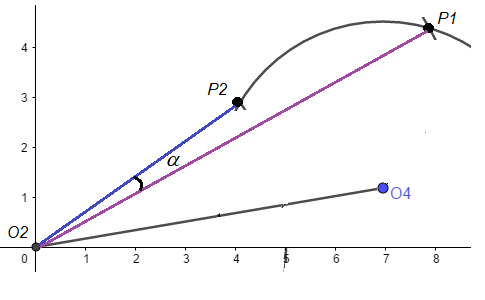
Figura 3. Parámetros relacionados con la relación de tiempo Q.

De la Figura 3, para una posición extrema hacia la derecha, el segmento O2P1 = L2 + L3, y para la posición extrema a la izquierda O2P2 = L3 – L2. Por lo tanto

O2P1 = L2 + L3        

O2P2 = L3 – L2        

O2P1- O2P2 = 2L2    (Ec 4)

Método gráfico para obtención de la relación de tiempo

Teniendo las longitudes del mecanismo L1,L2,L3 y L4 y el ángulo de inclinación θ1 del mecanismo de la Figura 1, así como los parámetros mostrados en la Figura 3 (B)

1. Dibujar el nodo O2 y O4 . O2 se puede localizar en coordenadas (0,0) y O4 se localiza usando L1 y θ1.

2. Dibujar un arco de circunferencia con el centro en O4 y radio la longitud L4

3. Dibujar un arco de circunferencia con el centro O2 y longitud L2+L3 y otro L3-L2, buscando la intersección con el arco anteriormente dibujado (ver Figura 3.B)

4. La intersección denotan los puntos P1 y P2 que son los extremos del oscilador, por lo tanto el ángulo formado por los segmentos O2P1 y O2P2 será el ángulo de la relación de tiempo α, de la cual es posible obtener la relación de tiempo Q, de la ecuación (Ec 3)

Created with the Personal Edition of HelpNDoc: Create cross-platform Qt Help files